算法

两数相加

题目描述

Leetcode:给定两个非空链表来表示两个非负整数。位数按照逆序方式存储，它们的每个节点只存储单个数字。将两数相加返回一个新的链表。

你可以假设除了数字 0 之外，这两个数字都不会以零开头。

示例：

输入：(2 -> 4 -> 3) + (5 -> 6 -> 4)
输出：7 -> 0 -> 8
原因：342 + 465 = 807

package com.xm.algorithm;

public class AddTwoNumber {

    public class ListNode {
        int val;
        ListNode next;

        ListNode(int x) {
            val = x;
        }
    }

    public  ListNode addTwoNumber(ListNode l1,ListNode l2) {
        ListNode p = l1;
        ListNode q = l2;
        int carry = 0;//用于表示进位

        //在这里先定义链表头，后面省去代码根据是不是第一次而创建头节点的问题
        ListNode headNode = new ListNode(0);
        ListNode curr = headNode;

        while(p!=null || q!=null) {
            int x = (p != null) ? p.val:0;
            int y = (q != null) ? q.val:0;
            int sum = x+y+carry;
            curr.next = new ListNode(sum%10);
            carry = sum/10;//只可能为0或1
            curr = curr.next;//往下继续
            if(p.next != null) p = p.next;
            if(q.next != null) q = q.next;
        }

        //最高位有进位
        if(carry > 0) {
            curr.next = new ListNode(carry);
        }
        return headNode.next;
    }
}

三数之和

leetcode 第 15 题

给一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？请你找出所有和为 0 且不重复的三元组。

注意：答案中不可以包含重复的三元组。

示例 1：

输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]

示例 2：

输入：nums = []
输出：[]

示例 3：

输入：nums = [0]
输出：[]

解题思路

题目中要求找到所有不重复且和为 0 的三元组，这个“不重复”的要求使得我们无法简单地使用三重循环枚举所有的三元组。这是因为在最坏的情况下，数组中的元素全部为 0，即：

[0, 0, 0, 0, 0, ..., 0, 0, 0]

任意一个三元组的和都为 0。如果直接使用三重循环枚举三元组，会得到 O(N^3) 个满足题目要求的三元组（其中 N 是数组的长度）,时间复杂度至少为 O(N^3)。在这之后，还需要使用哈希表进行去重操作，得到不包含重复三元组的最终答案，又消耗了大量的空间。这个做法的时间复杂度和空间复杂度都很高，因此我们要换一种思路来考虑这个问题。

「不重复」的本质是什么？我们保持三重循环的大框架不变，只需要保证：

• 第二重循环枚举到的元素不小于当前第一重循环枚举到的元素；

• 第三重循环枚举到的元素不小于当前第二重循环枚举到的元素。

也就是说，枚举的三元组 (a, b, c)满足 a≤b≤c，保证了只有(a,b,c) 这个顺序会被枚举到，而(b,a,c)、(c,b,a) 等等这些不会，这样就减少了重复。要实现这一点，可以将数组中的元素从小到大进行排序，随后使用普通的三重循环就可以满足上面的要求。

同时，对于每一重循环而言，相邻两次枚举的元素不能相同，否则也会造成重复。举个例子，如果排完序的数组为

[0, 1, 2, 2, 2, 3]
 ^  ^  ^

我们使用三重循环枚举到的第一个三元组为 (0,1,2)，如果第三重循环继续枚举下一个元素，那么仍然是三元组 (0,1,2)，产生了重复。因此我们需要将第三重循环「跳到」下一个不相同的元素，即数组中的最后一个元素 3，枚举三元组 (0,1,3)。

伪代码如下：

nums.sort()
for first = 0 .. n-1
    // 只有和上一次枚举的元素不相同，我们才会进行枚举
    if first == 0 or nums[first] != nums[first-1] then
        for second = first+1 .. n-1
            if second == first+1 or nums[second] != nums[second-1] then
                for third = second+1 .. n-1
                    if third == second+1 or nums[third] != nums[third-1] then
                        // 判断是否有 a+b+c==0
                        check(first, second, third)

这种方法的时间复杂度仍然为 O(N^3)，毕竟还是没有跳出三重循环的大框架。然而它是很容易继续优化的，可以发现，可以发现，如果我们固定了前两重循环枚举到的元素 a 和 b，那么只有唯一的 c 满足 a+b+c=0。当第二重循环往后枚举一个元素 b’ 时，由于 b’ > b，那么满足 a+b’+c’=0 的 c’ 一定有 c’ < c，即 c’ 在数组中一定出现在 c 的左侧。也就是说，我们可以从小到大枚举 b，同时从大到小枚举 c ，即第二重循环和第三重循环实际上是并列的关系。

有了这样的发现，我们就可以保持第二重循环不变，而将第三重循环变成一个从数组最右端开始向左移动的指针，从而得到下面的伪代码：

nums.sort()
for first = 0 .. n-1
    if first == 0 or nums[first] != nums[first-1] then
        // 第三重循环对应的指针
        third = n-1
        for second = first+1 .. n-1
            if second == first+1 or nums[second] != nums[second-1] then
                // 向左移动指针，直到 a+b+c 不大于 0
                while nums[first]+nums[second]+nums[third] > 0
                    third = third-1
                // 判断是否有 a+b+c==0
                check(first, second, third)

这个方法就是我们常说的「双指针」，当我们需要枚举数组中的两个元素时，如果我们发现随着第一个元素的递增，第二个元素是递减的，那么就可以使用双指针的方法，将枚举的时间复杂度从 O(N^2) 减少至 O(N)。为什么是 O(N)呢？这是因为在枚举的过程每一步中，「左指针」会向右移动一个位置（也就是题目中的 b），而「右指针」会向左移动若干个位置，这个与数组的元素有关，但我们知道它一共会移动的位置数为 O(N)，均摊下来，每次也向左移动一个位置，因此时间复杂度为 O(N)。

注意到我们的伪代码中还有第一重循环，时间复杂度为 O(N)，因此枚举的总时间复杂度为 O(N^2)。由于排序的时间复杂度为 O(N \log N)，在渐进意义下小于前者，因此算法的总时间复杂度为 O(N^2)。

上述的伪代码中还有一些细节需要补充，例如我们需要保持左指针一直在右指针的左侧（即满足 b*≤*c），具体可以参考下面的代码，均给出了详细的注释。

代码实现

func threeSum(nums []int) [][]int {
    var ret [][]int
    length := len(nums)
    sort.Ints(nums)

    for i := 0; i < length; i++ {
        // 跟上一次相同的值可以跳过
        if i != 0 && nums[i] == nums[i-1] {
            continue
        }
        // 双指针遍历，这里左指针是j，右指针是k
        k := length - 1
        for j := i + 1; j < length; j++ {
            // 同样，跟上一次相同就略过，只需要看不同的
            if j != i+1 && nums[j] == nums[j-1] {
                continue
            }
            // 保持左指针不大于右指针，注意这里要大于0，如果已经小于0那就跳过了，后面都会一直小于0
            for j < k && nums[i]+nums[j]+nums[k] > 0 {
                k--
            }
            // 如果指针重合，由于在 a 不变的情况下，随着 b 的增加，c 只能减少，所以后续不会再有 a+b+c=0
            // 此时可以退出本次循环
            if j == k {
                break
            }
            if nums[i]+nums[j]+nums[k] == 0 {
                ret = append(ret, []int{nums[i], nums[j], nums[k]})
            }
        }
    }
    return ret
}

最接近的三数之和

Leetcode 第 16 题

给定一个包括 n 个整数的数组 nums 和 一个目标值 target。找出 nums 中的三个整数，使得它们的和与 target 最接近。返回这三个数的和。假定每组输入只存在唯一答案。

输入：nums = [-1,2,1,-4], target = 1
输出：2
解释：与 target 最接近的和是 2 (-1 + 2 + 1 = 2) 。

解题思路

这道题最简单的思路就是直接暴力破解。但是更好的解法也是和上面的三数之和一样，采用双指针夹逼的方式来遍历，所以首先需要先让数组有序。具体思路参考上一题。

代码实现

// 双指针夹逼法
func threeSumClosest(nums []int, target int) int {
    // 记录最接近的和（不要用MaxInt64，防止没有空间导致溢出）
    closest := math.MaxInt32
    // 生序排序
    sort.Ints(nums)
    for i := 0; i < len(nums)-2; i++ {
        // 保证和上一次枚举的元素不相等
        if i > 0 && nums[i] == nums[i-1] {
            continue
        }

        lp, rp := i+1, len(nums)-1
        // 保证左指针小于右指针
        for lp < rp {
            // 如果和为 target 直接返回答案
            sum := nums[i] + nums[lp] + nums[rp]
            if sum == target {
                return sum
            }
            if abs(sum-target) < abs(closest-target) {
                closest = sum
            }
            // 相同数直接跳过
            if sum < target {
                lp++
                for lp < rp && nums[lp] == nums[lp-1] {
                    lp++
                }
            } else {
                rp--
                for lp < rp && nums[rp] == nums[rp+1] {
                    rp--
                }
            }
        }
    }
    return closest
}

func abs(x int) int {
    if x < 0 {
        return -1 * x
    }
    return x
}

• 时间复杂度：O(N^2)，其中 N 是数组 nums 的长度。我们首先需要 O*(NlogN) 的时间对数组进行排序，随后在枚举的过程中，使用一重循环 O(N) 枚举 a，双指针 O(N) 枚举 b 和 c，故一共是 O(*N2)。
• 空间复杂度 O*(logN)。排序需要使用 O(log*N) 的空间。然而我们修改了输入的数组nums，在实际情况下不一定允许，因此也可以看成使用了一个额外的数组存储了nums 的副本并进行排序，此时空间复杂度为 O(N)。

四数之和

leetcode 第 18 题

给你一个由 n 个整数组成的数组 nums ，和一个目标值 target 。请找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]] （若两个四元组元素一一对应，则认为两个四元组重复）：

• 0 <= a, b, c, d < n
• a、b、c 和 d 互不相同
• nums[a] + nums[b] + nums[c] + nums[d] == target

示例 1：

输入：nums = [1,0,-1,0,-2,2], target = 0
输出：[[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]]

示例 2：

输入：nums = [2,2,2,2,2], target = 8
输出：[[2,2,2,2]]

解题思路

这道题的思路跟三数之和类似，也是采用排序加双指针的方式来解题，不同在于其外层有两个循环，因为是四个数的和。

代码实现

func fourSum(nums []int, target int) [][]int {
    var ret [][]int
    sort.Ints(nums)
    n := len(nums)

    // 第一重循环
    for i := 0; i < n-3 && nums[i]+nums[i+1]+nums[i+2]+nums[i+3] <= target; i++ {
        if i > 0 && nums[i] == nums[i-1] || nums[i]+nums[n-3]+nums[n-2]+nums[n-1] < target {
            continue
        }
        // 第二重循环
        for j := i + 1; j < n-2 && nums[i]+nums[j]+nums[j+1]+nums[j+2] <= target; j++ {
            if j > i+1 && nums[j] == nums[j-1] || nums[i]+nums[j]+nums[n-2]+nums[n-1] < target {
                continue
            }
            // 左指针
            for lp := j + 1; lp < n-1 && nums[i]+nums[j]+nums[lp]+nums[lp+1] <= target; lp++ {
                if lp > j+1 && nums[lp] == nums[lp-1] || nums[i]+nums[j]+nums[lp]+nums[n-1] < target {
                    continue
                }
                rp := n - 1 // 右指针
                for rp > lp && (nums[i]+nums[j]+nums[lp]+nums[rp] > target) {
                    rp--
                }
                if lp == rp {
                    break
                }
                if nums[i]+nums[j]+nums[lp]+nums[rp] == target {
                    ret = append(ret, []int{nums[i], nums[j], nums[lp], nums[rp]})
                }
            }
        }
    }
    return ret
}

复杂度分析

• 时间复杂度：O(n^3)，其中 n 是数组的长度。排序的时间复杂度是 O(nlogn)，枚举四元组的时间复杂度是 O*(*n3)，因此总时间复杂度为 O(n^3+n log n)=O(n^3)。
• 空间复杂度：O*(logn)，其中 n 是数组的长度。空间复杂度主要取决于排序额外使用的空间。此外排序修改了输入数组 nums，实际情况中不一定允许，因此也可以看成使用了一个额外的数组存储了数组 nums 的副本并排序，空间复杂度为 O(*n)。

连续子数组的最大和

剑指 Offer 31 题

题目：输入一个整型数组，数组里有正数也有负数。数组中一个或连续的多个整数组成一个子数组。求所有子数组的和的最大值。

要求时间复杂度为O（n）。

例如输入的数组为 {1,-2,3,10,-4,7,2,-5}，其和最大的子数组为 {3,10,-4, 7,2}，因此输出为该子数组的和18。

解题思路

这道题可以使用动态规划的方式，如果用函数 f(i) 表示以第 i 个数字结尾的子数组的最大和，那么需要求出 max[f(i)]，其中 0≤i<n。

那么 f(i) 有下面两种情况：

f(i) = pData[i] (i=0或者f(i-1)<=0)
f(i) = f(i-1)+pData[i]

当以第 i-1 个数字结尾的子数组中所有数字的和小于 0 时，如果把这个负数与第 i 个数累加，得到的结果比第 i 个数字本身还要小，所以这种情况下以第 i 个数字结尾的子数组就是第 i 个数字本身。如果以第 i-1 个数字结尾的子数组中所有数字的和大于 0，与第 i 个数字累加就得到以第 i 个数字结尾的子数组中所有数字的和。

代码实现

func maxSubArray(nums []int) int {
    var ret = nums[0]
    var curr int
    for i := 0; i < len(nums); i++ {
        if curr >= 0 {
            curr += nums[i]
        } else {
            curr = nums[i]
        }
        if curr >= ret {
            ret = curr
        }
    }
    return ret
}

求斐波纳切数列的第n个数/爬楼梯

Leecode:假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢

写一个函数，输入 n ，求斐波那契（Fibonacci）数列的第 n 项（即 F(N)）。斐波那契数列的定义如下：

F(0) = 0, F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
斐波那契数列由 0 和 1 开始，之后的斐波那契数就是由之前的两数相加而得出。

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

分析：

动态规划思想，爬上最后一层楼梯可能是差一阶或两阶，即f(N)=f(N-1)+f(N-2)，此时数列变成”1 1 2 3 5 …”

class Solution {
    public int fib(int N) {
        if(N<1) {
            return 0;
        }
        if(N==1 || N==2) {
              // 斐波那契数列
              return 1;
              // 爬楼梯
            return N;
        }

        int f1 = 1;
          // 斐波那契数列
        int f2 = 1;
          // 爬楼梯
          int f2 = 2;
        int result = 0;
        for(int i=3;i<=N;i++) {
            result = f1 +f2;
            f1 = f2;
            f2 = result;
        }
        return result;
    }
}

另外，在斐波哪切数列中，还需要注意数值超过最大范围的情况，所以每次求完值都进行一次求余操作

go 解法：

func fib(n int) int {
    const mod int = 1e9 + 7
    if n < 2 {
        return n
    }
    p, q, r := 0, 0, 1
    for i := 2; i <= n; i++ {
        p = q
        q = r
        r = (p + q) % mod
    }
    return r
}

变态台阶问题

题目描述：

一只青蛙一次可以跳上1级台阶，也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

问题分析：

假设 n>=2，第一步有n种跳法：跳 1 级、跳 2 级,到跳 n 级。 跳 1 级，剩下 n-1 级，则剩下跳法是 f(n-1)； 跳 2 级，剩下 n-2 级，则剩下跳法是 f(n-2) …… 跳 n-1 级，剩下 1 级，则剩下跳法是 f(1)； 跳 n 级，剩下 0 级，则剩下跳法是 f(0)

所以在 n>=2 的情况下： f(n)=f(n-1)+f(n-2)+...+f(1) 因为 f(n-1)=f(n-2)+f(n-3)+...+f(1),所以 f(n)=2*f(n-1), 又 f(1)=1,所以可得 f(n)=2^(number-1)

示例代码：

int JumpFloorII(int number) {
    return 1 << --number;//2^(number-1)用位移操作进行，更快
}

求比整数N小的所有正整数中，各位数字乘积最大者，如输入220，返回199

public class MaximumProduct {

    /**
     * 求出最大乘积是多少
     * @param number
     * @return
     */
    private int getMaximumProduct(int number) {
        if(number == 0){
            return 1;
        } else if(number < 10) {
            return number;
        } else {
           return Math.max(getMaximumProduct(number / 10) * (number % 10),getMaximumProduct(number / 10 -1) * 9);
        }
    }

    private int solve(int number) {
        
        //用于存储每一位数
        List<Integer> list = new ArrayList<>();
        int result = 0;

        while (number > 0){
            //获取除个位数以外的部分
            int n = number/10;
            //个位数取9时，高位部分减1
            int m = number/10-1;
            //比较个位数取 9 和按原数计算哪个数乘积比较大
            if(getMaximumProduct(n) * (number%10) < getMaximumProduct(m) * 9) {
                //个位数取9比较大，存入数组，相应的把number变为高位部分，继续比较
                number = m;
                list.add(9);
            } else {
                //原数大，则存入数组，相应把number变为高位部分，继续比较
                list.add(number%10);
                number = n;
            }
        }
        int size = list.size();
        for (int i = size-1; i >= 0; i--) {
            result = result * 10 + list.get(i);
        }
        return result;
    }
}

1-N 这些数中1出现的次数

Leecode: 给定一个整数 n，计算所有小于等于 n 的非负整数中数字 1 出现的个数。

示例：

输入: 13
输出: 6 
解释: 数字 1 出现在以下数字中: 1, 10, 11, 12, 13 。

解法一：暴力破解

思路：

1. 将 i 从 1 遍历到 n：
2. 将 i 转成字符串，数 ’1’ 的个数
3. 将每个字符串里 ’1’ 的个数累加到变量 countr
4. 返回 countr

public int countDigitOne(int n) {
    int count = 0;
    for (int i = 0; i <= n; i++) {
        String s1 = String.valueOf(i);
        int len1 = s1.length();
        String s2 = s1.replaceAll("1", "");
        int len2 = s2.length();
        count += (len1 - len2);
    }
    return count;
}

复杂度分析:

• 时间复杂度：O(n*log10(n))：从 1 遍历到 n 每次遍历中，我们把整数转成字符串去数 ’1’ 的个数，这个过程会花费 m 的时间，其中 m 为字符串的长度，其最大值为 log10(n)。
• 空间复杂度：需要申请O(log10(n)) 个额外的空间来存储 countr 和整数转换成的字符串 str。

数学法

下面的图列出了求个位数，十位数，百位数…的规则:

由上图所示，可以观察到每 10 个数，个位上的 ’1’ 就会出现一次。同样的，每 100 个数，十位上的 ’1’ 就会出现一次。这个规律可以用 (n/(10^i))*(10^i) 公式来表示。（i 标识

同时，如果十位上的数是 ’1’，那么最后 ’1’ 的数量要加上 x+1，其中 x 是个位上的数值。如果十位上的数大于 ’1’，那么十位上为 ’1’ 的所有的数都是符合要求的，这时候最后 ’1’ 的数量要加 10。

这个规律可以用公式 min(max((n mod (10^i))−(10^(i-1))+1,0),10^(i-1)) 来表示。

来看一个例子，有一个数 n=1234。

个位上 ’1’ 的数量 = 1234/10 (对应 1,11,21,...1221) + min(4,1) (对应 1231) = 124

十位上 ’1’ 的数量 = (1234/100)*10 (对应 10,11,12,...,110,111,...1919) + min(25, 10) (对应 1210,1211,...1219) = 130

百位上 ’1’ 的数量 = (1234/1000)*100 (对应 100,101,102,...,199) + min(135, 100) (对应1100,1101...1199) = 200

千位上 ’1’ 的数量 = (1234/10000)*10000 + min(235, 1000) (对应1000,1001,...1234) = 235

因此，总数 = 124+130+200+235 = 689。

算法实现：

• 将 i 从 1 遍历到 n，每次遍历 i 扩大 10 倍：
• (n/(i*10))*i 表示 (i*10) 位上 ’1’ 的个数。
• {min(max(({n mod (i*10)} )-i+1,0),i)} 表示需要额外数的 (i*10) 位上 ’1’ 的个数。

int countDigitOne(int n) {
    int count = 0;
    for (long i = 1; i <= n; i *= 10) {
        long divider = i * 10;
        count += (n / divider) * i + Math.min(Math.max(n % divider - i + 1, 0L), i);
    }
    return count;
}

复杂度分析

• 时间复杂度：O(log10(n)),遍历的次数等于 n 转成字符串后字符串的长度，其值为 log10(n)。
• 空间复杂度：只需要 O(1) 的额外空间。

二进制中 1 的个数

剑指 offer 第 15 题：编写一个函数，输入是一个无符号整数（以二进制串的形式），返回其二进制表达式中数字位数为 ‘1’ 的个数（也被称为 汉明重量).）。

提示：

请注意，在某些语言（如 Java）中，没有无符号整数类型。在这种情况下，输入和输出都将被指定为有符号整数类型，并且不应影响您的实现，因为无论整数是有符号的还是无符号的，其内部的二进制表示形式都是相同的。
在 Java 中，编译器使用 二进制补码 记法来表示有符号整数。因此，在上面的 示例 3 中，输入表示有符号整数 -3。

示例 1：

输入：n = 11 (控制台输入 00000000000000000000000000001011)
输出：3
解释：输入的二进制串 00000000000000000000000000001011 中，共有三位为 ‘1’。

示例 2：

输入：n = 128 (控制台输入 00000000000000000000000010000000)
输出：1
解释：输入的二进制串 00000000000000000000000010000000 中，共有一位为 ‘1’。

示例 3：

输入：n = 4294967293 (控制台输入 11111111111111111111111111111101，部分语言中 n = -3）
输出：31
解释：输入的二进制串 11111111111111111111111111111101 中，共有 31 位为 ‘1’。

解析

这道题比较容易想到的方法就是每次把数字左移，每次与1进行 & 判断，但是这种方式，在遇到负数的时候，容易引起死循环：

func hammingWeight(num uint32) int {
    count := 0
    for num != 0 {
        if num & 1 == 1{
            count++
        }
        num = num>>1
    }
    return count
}

为了避免死循环，可以不右移输入的数字num。首先把num和1做与运算，判断num的最低位是不是为1。接着把1左移一位得到2，再和num做与运算，就能判断num的次低位是不是1……这样反复左移，每次都能判断num的其中一位是不是1。

func hammingWeight(num uint32) (ones int) {
    for i := 0; i < 32; i++ {
        if 1<<i&num > 0 {
            ones++
        }
    }
    return
}

这个解法中循环的次数等于整数二进制的位数，32 位的整数需要循环32次。

• 时间复杂度：O(k)，其中 k 是 int 型的二进制位数，k=32。我们需要检查 n 的二进制位的每一位，一共需要检查 32 位。

• 空间复杂度：O(1)，我们只需要常数的空间保存若干变量。

还有一种更为巧妙的解法，在这种解法中，整数中有几个1就只需要循环几次。

如果一个整数不等于0，那么该整数的二进制表示中至少有一位是1。先假设这个数的最右边一位是1，那么减去1时，最后一位变成0而其他所有位都保持不变。也就是最后一位相当于做了取反操作，由1变成了0。

接下来假设最后一位不是1 而是0 的情况。如果该整数的二进制表示中最右边1位于第m位，那么减去1时，第m位由1变成0，而第m位之后的所有0都变成1，整数中第m位之前的所有位都保持不变。举个例子：一个二进制数 1100，它的第二位是从最右边数起的一个 1。减去 1 后，第二位变成0，它后面的两位0变成1，而前面的1保持不变，因此得到的结果是1011。在前面两种情况中，我们发现把一个整数减去1，都是把最右边的1变成0。如果它的右边还有0的话，所有的0都变成1，而它左边所有位都保持不变。接下来我们把一个整数和它减去 1 的结果做位与运算，相当于把它最右边的1变成0。还是以前面的1100为例，它减去1的结果是1011。我们再把1100和1011做位与运算，得到的结果是1000。我们把1100最右边的1变成了0，结果刚好就是1000。

总的来说，就是把一个整数减去1，再和原整数做与运算，会把该整数最右边一个1变成0。那么一个整数的二进制表示中有多少个1，就可以进行多少次这样的操作：

func hammingWeight(num uint32) (ones int) {
    for ; num > 0; num &= num - 1 {
        ones++
    }
    return
}

• 时间复杂度：O(logn)。循环次数等于 nn 的二进制位中 1 的个数，最坏情况下 n 的二进制位全部为 1。我们需要循环 logn 次。
• 空间复杂度：O(1)，我们只需要常数的空间保存若干变量。

数值的整数次方

剑指 Offer 16 题： 实现 pow(x, n) ，即计算 x 的 n 次幂函数（即，xn）。不得使用库函数，同时不需要考虑大数问题。

示例 1：

输入：x = 2.00000, n = 10
输出：1024.00000

示例 2：

输入：x = 2.10000, n = 3
输出：9.26100

示例 3：

输入：x = 2.00000, n = -2
输出：0.25000
解释：2-2 = 1/22 = 1/4 = 0.25

实现思路

在实现的时候首先需要考虑 n 是正数还是负数，如果是负数，应该将 n 取绝对值，将负号提到 x 中。

假设输入的 n 是 32，即要求 x 的 32 次方，如果我们已经知道了它的16次方，那么只要在16次方的基础上再平方一次就可以了。而16次方是8次方的平方。这样以此类推，我们求32次方只需要做5次乘法：先求平方，在平方的基础上求4次方，在4次方的基础上求8次方，在8次方的基础上求16次方，最后在16次方的基础上求32次方。也就是说，可以用如下公式求a的n次方：

代码实现

递归实现

func myPow(x float64, n int) float64 {
    if n == 0 {
        return 1
    }
    if n == 1 {
        return x
    }

    flag := n < 0
    if flag {
        n = -n
    }

    var result float64
    result = myPow(x, n>>1)
    result = result * result
    if n&1 == 1{
        result = result * x
    }

    if flag {
        return 1 / result
    }
    return result
}

迭代实现

func myPow(x float64, n int) float64 {
    var flag bool
    if n < 0 {
        n = -n
        flag = true
    }

    var ret = 1.0
    var pow = x

    // 循环到最后肯定有一个 1，因此计数最少有一次
    // 对于一开始指数是单数的场景，最后计数是两次
    // 对于一开始指数是双数的场景，最后计数是一次
    for n > 0 {
        if n&1 == 1 {
            ret *= pow
        }
        pow *= pow
        n >>= 1
    }
    if flag {
        return 1 / ret
    }
    return ret
}

整数转罗马数字

Leetcode 第 12 题

罗马数字包含以下七种字符： I， V， X， L，C，D 和 M。

字符          数值
I             1
V             5
X             10
L             50
C             100
D             500
M             1000

例如， 罗马数字 2 写做 II ，即为两个并列的 1。12 写做 XII ，即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。

通常情况下，罗马数字中小的数字在大的数字的右边。但也存在特例，例如 4 不写做 IIII，而是 IV。数字 1 在数字 5 的左边，所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地，数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况：

• I 可以放在 V (5) 和 X (10) 的左边，来表示 4 和 9。

• X 可以放在 L (50) 和 C (100) 的左边，来表示 40 和 90。

• C 可以放在 D (500) 和 M (1000) 的左边，来表示 400 和 900。

给一个整数，将其转为罗马数字。

解题思路

罗马数字由 7 个不同的单字母符号组成，每个符号对应一个具体的数值。此外，减法规则（如问题描述中所述）给出了额外的 6 个复合符号。这给了我们总共 13 个独特的符号（每个符号由 1 个或 2 个字母组成），如下图所示。

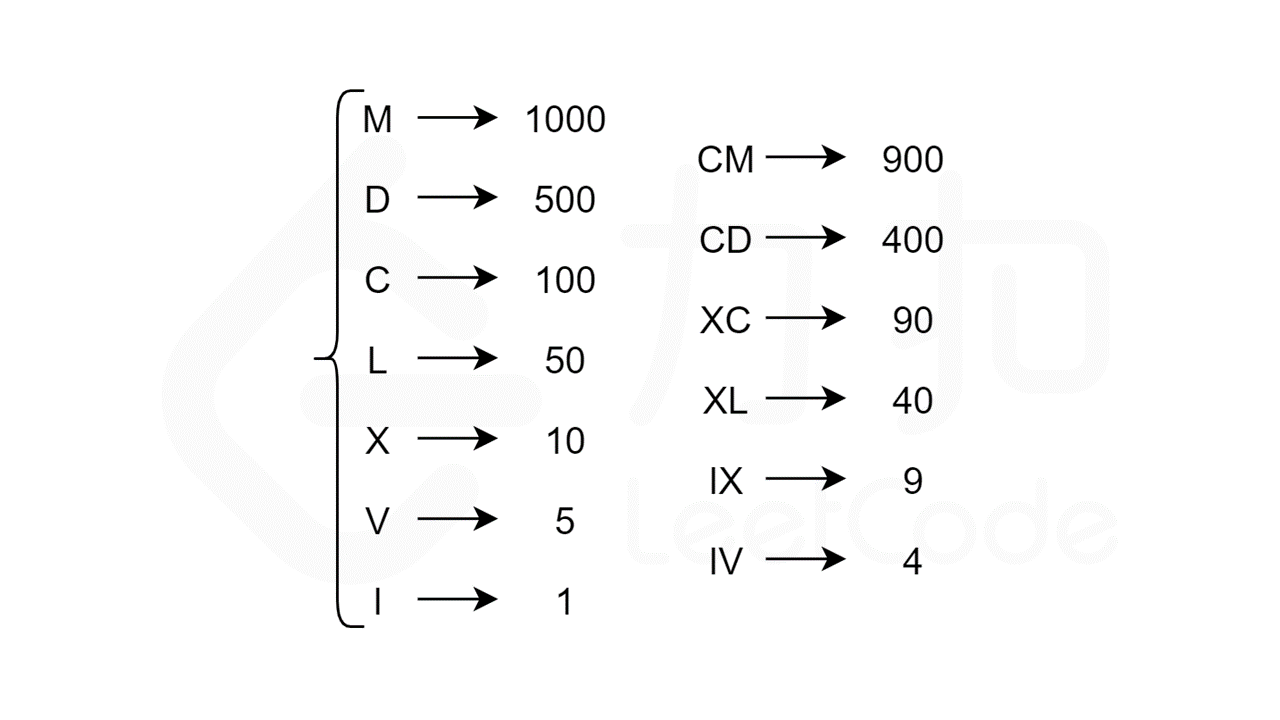
用来确定罗马数字的规则是：对于罗马数字从左到右的每一位，选择尽可能大的符号值。对于 140，最大可以选择的符号值为 C=100。接下来，对于剩余的数字 40，最大可以选择的符号值为 XL=40。因此，140 的对应的罗马数字为 C+XL=CXL。

根据罗马数字的唯一表示法，为了表示一个给定的整数 num，寻找不超过 num 的最大符号值，将 num 减去该符号值，然后继续寻找不超过 num 的最大符号值，将该符号拼接在上一个找到的符号之后，循环直至 num 为 0。最后得到的字符串即为 num 的罗马数字表示。

编程时，可以建立一个数值-符号对的列表，按数值从大到小排列。遍历映射表中的每个数值-符号对，若当前数值 value 不超过 num，则从 num 中不断减去 value，直至 num 小于 value，然后遍历下一个数值-符号对。若遍历中 num 为 0 则跳出循环。

代码实现

// 罗马数字与数字的映射关系
var numRomanMap = []struct {
    value  int
    symbol string
}{
    {1000, "M"},
    {900, "CM"},
    {500, "D"},
    {400, "CD"},
    {100, "C"},
    {90, "XC"},
    {50, "L"},
    {40, "XL"},
    {10, "X"},
    {9, "IX"},
    {5, "V"},
    {4, "IV"},
    {1, "I"},
}

func intToRoman(num int) string {
    var ret []byte
    // 循环映射表，以此减去最大的部分
    for _, nummap := range numRomanMap {
        for num >= nummap.value {
            ret = append(ret,nummap.symbol...)
            num = num-nummap.value
        }
        if num == 0 {
            return string(ret)
        }
    }
    return string(ret)
}

• 时间复杂度：O(1)。由于映射表的长度是固定的，且这 13 字符中的每个字符的出现次数均不会超过 3，因此循环次数有一个确定的上限。对于本题给出的数据范围，循环次数不会超过 15 次。
• 空间复杂度：O(1)。

TOP K 问题

从 1 亿个数中找出最大的前 100 个。

堆排

利用小顶堆，首先遍历 100 个数放入堆中，后面每次遍历与堆顶比较，比堆顶大就替换堆顶并对堆进行调整。

堆排的时间复杂度是n*logn,适用场景：

• 不会改变数据的输入顺序（按顺序读的）；
• 不会占用太多的内存空间（事实上，一次只读入一个数，内存只要求能容纳前K个数即可）；
• 由于（2），决定了它特别适合处理海量数据。

public class TopK {

    public static void main(String[] args) {
        
        //假设这是给定的数据
        int[] a = { 1, 17, 3, 4, 5, 6, 7, 16, 9, 10, 11, 12, 13, 14, 15, 8 };
        //寻找前4个最大的数
        int[] b = topK(a, 4);
        for (int i = 0; i < b.length; i++) {
            System.out.print(b[i] + ", ");
        }
    }

    //对堆的 index 节点进行调整使其符合小顶堆定义
    public static void heapify(int[] array, int index, int length) {
        int left = index * 2 + 1;//左孩子
        int right = index * 2 + 2;//右孩子
        int smallest = index;
        if (left < length && array[left] < array[index]) {
            smallest = left;
        }
        if (right < length && array[right] < array[smallest]) {
            smallest = right;
        }
        if (index != smallest) {
            swap(array, smallest, index);
            //递归往下继续调整
            heapify(array, smallest, length);
        }
    }

    public static void swap(int[] array, int a, int b) {
        int temp = array[a];
        array[a] = array[b];
        array[b] = temp;
    }

    /**
     * 初始化小顶堆
     */
    public static void buildHeap(int[] array) {
        int length = array.length;
        /** 
         * 由于单个结点的完全二叉树满足堆的特性，所以叶子结点都是堆。因此可以忽略叶子结点元素
         * 对 n 个结点的完全二叉树建堆的过程是：依次将编号为 n/2,n/2-1,...1 的结点为根的子树筛选为子堆
         */
        for (int i = length / 2 - 1; i >= 0; i--) {
            heapify(array, i, length);
        }
    }

    /**
     * 设置新的堆顶
     */
    public static void setTop(int[] array, int top) {
        array[0] = top;
        heapify(array, 0, array.length);
    }

    public static int[] topK(int[] array, int k) {
        int[] top = new int[k];
        for (int i = 0; i < k; i++) {
            top[i] = array[i];
        }
        //先建堆，然后依次比较剩余元素与堆顶元素的大小，比堆顶小的， 说明它应该在堆中出现，则用它来替换掉堆顶元素，然后沉降。
        buildHeap(top);
        for (int j = k; j < array.length; j++) {
            int temp = top[0];
            if (array[j] > temp) {
                setTop(top, array[j]);
            }
        }
        return top;
    }
}

快排方式

分治函数会返回一个 position，在 position 左边的数都比第 position 个数小，在 position 右边的数都比第 position 大。通过不断调用分治函数，直到它输出的 position = K-1，此时 position 前面的K个数（0到K-1）就是要找的前K个数。

时间复杂度为 n ，特点：

• partition函数会不断地交换元素的位置，所以它肯定会改变数据输入的顺序；
• 既然要交换元素的位置，那么所有元素必须要读到内存空间中，所以它会占用比较大的空间，至少能容纳整个数组；
• 数据越多，占用的空间必然越大，海量数据处理起来相对吃力。

public class TopK {

    public static void main(String[] args) {
        // TODO Auto-generated method stub
        int[] array = { 9, 3, 1, 10, 5, 7, 6, 2, 8, 0 };
        getTopK(array, 4);
        for (int i = 0; i < array.length; i++) {
            System.out.print(array[i] + ", ");
        }
    }

    /**
     * 从数组的右端向左扫描找到第一个大于它的元素，将这个元素放在 `l` 位置，
     * 从数组的左端向右扫描直到找到第一个小于等于枢轴的元素，
     * 放到右边高端刚交换完空出的位置。
     * 不断进行这个过程，就可以保证左指针 i 的左侧元素都不小于切分元素，
     * 右指针 j 的右侧元素都不大于切分元素。
     * 当两个指针相遇时，将枢轴的值放到该位置。
     */
    public static int partition(int[] array, int low, int high) {
        if (array != null && low < high) {
            int flag = array[low];
            while (low < high) {
                while (low < high && array[high] <= flag) {
                    high--;
                }
                array[low] = array[high];
                while (low < high && array[low] >= flag) {
                    low++;
                }
                array[high] = array[low];
            }
            array[low] = flag;
            return low;
        }
        return 0;
    }

    public static void getTopK(int[] array, int k) {
        if (array != null && array.length > 0) {
            int low = 0;
            int high = array.length - 1;
            int index = partition(array, low, high);
            //不断调整分治的位置，直到position = k-1
            while (index != k - 1) {
                //大了，往前调整
                if (index > k - 1) {
                    high = index - 1;
                    index = partition(array, low, high);
                }
                //小了，往后调整
                if (index < k - 1) {
                    low = index + 1;
                    index = partition(array, low, high);
                }
            }
        }
    }
}

go 版本实现（最小的 k 个数）:

func getLeastNumbers(arr []int, k int) []int {
    if len(arr) < k || k == 0 {
        return nil
    }

    start := 0
    end := len(arr) - 1
    pivotloc := quickSort(arr, start, end)
    for pivotloc != k-1 {
        if pivotloc > k-1 {
            end = pivotloc - 1
            pivotloc = quickSort(arr, start, end)
        } else {
            start = pivotloc + 1
            pivotloc = quickSort(arr, start, end)
        }
    }
    return arr[:k]
}

func quickSort(arr []int, start, end int) int {
    var l = start
    var r = end
    var val = arr[l]
    for l < r {
        for l != r && arr[r] >= val {
            r--
        }
        arr[l] = arr[r]
        for l != r && arr[l] < val {
            l++
        }
        arr[r] = arr[l]
    }
    arr[l] = val
    return l
}

空间换时间：bitmap方式(海量数据排序也可以用)

bitmap（比特位图法），是空间换时间的典型代表。它是一种，用若干个 bit 来表示集合的数据结构。

例如，集合S={1,3,5,7,9}，容易发现，S中所有元素都在1-16之间，于是，可以用16个bit来表示这个集合：存在于集合中的元素，对应bit置1，否则置0。

上述集合S，可以用1010101010000000这样一个16bit的bitmap来表示，其中，第1, 3, 5, 7, 9个bit位置是1。

假设TopK的n个元素都是int，且元素之间没有重复，只需要申请2^32个bit，即4G的内存，就能够用bitmap表示这n元素。

扫描一次所有n个元素，以生成bitmap，其时间复杂度是O(n)。生成后，取TopK只需要找到最高位的k个bit即可。算法总时间复杂度也是O(n)。

bitmap 算法有一个缺陷，如果集合元素有重复，相同的元素会被去重，如果需要考虑重复元素，则需要通过比特位图精准计数的方式：

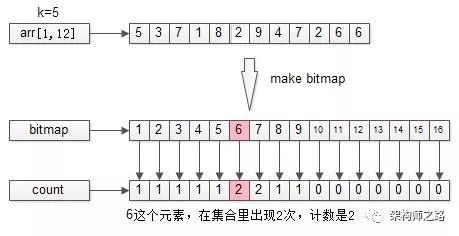
TopK的集合经过比特位图计数处理后，会记录每个bit对应在集合S中出现过多少次。

接下来，找TopK的过程，就是bitmap从高位的计数开始，往低位的计数扫描，得到count之和等于k，对应的bit就是TopK所求。

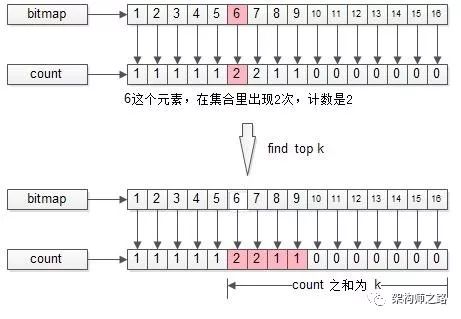
如上图所示，k=5：

1. 第一个非0的count是1，对应的bit是9；
2. 第二个非0的count也是1，对应的bit是8；
3. 第三个非0的count是2，对应的bit是7；
4. 第四个非0的count是2，对应的bit是6，但TopK只缺1个数字了，故只有1个6入选；

故，最终的TopK={9, 8, 7, 7, 6}。

结论：通过比特位图精准计数的方式，求解TopK，算法整体只需要不到2次扫描，时间复杂度为O(n)，比减治法的随机选择会更快。

1亿个 IPV 地址找相同

方法一：hash取模

按照IP地址的 hash(IP)%1024 值，将海量日志存储到 1024 个小文件中，每个小文件最多包含 4M 个IP地址(IP地址最多有 2^32=4G 种取值可能)。

对于每个小文件，可以构建一个 IP 作为 key，出现次数作为 value 的hash_map，并记录当前出现次数最多的 1 个 IP 地址。有了 1024 个小文件中的出现次数最多的 IP，我们就可以轻松得到总体上出现次数最多的 IP。

方法二：bitmap

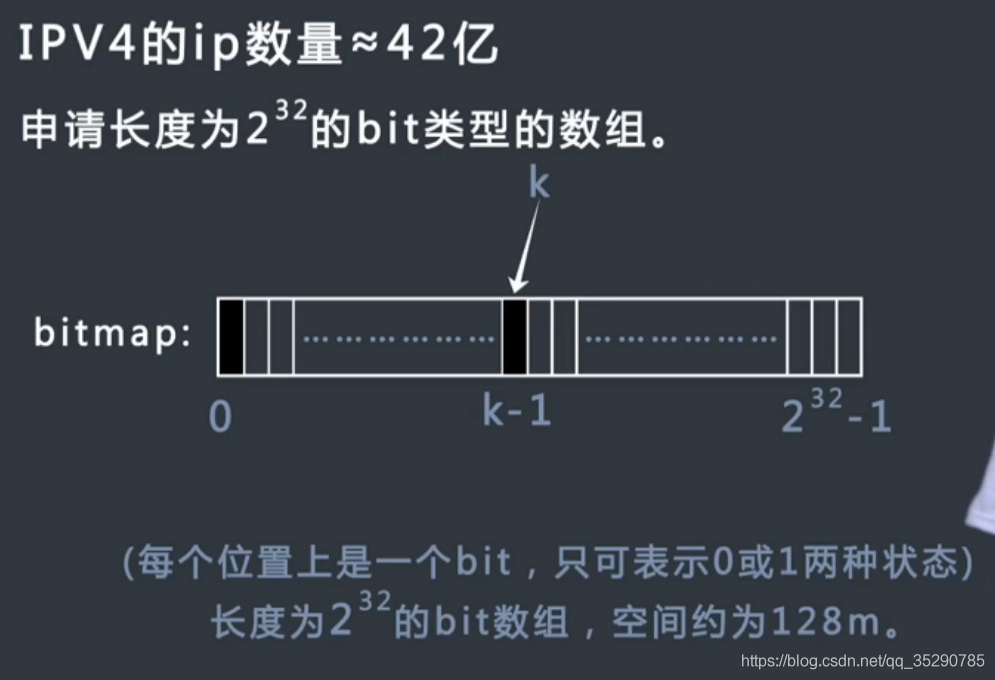
申请一个长度为2^32的bit类型的数组，每个位置上是一个bit，只可表示0或者1两种状态，空间为 512 M。

每个 IP 地址转化成无符号整数 k，数组下标 0~2^32-1 与 k 对应起来。如果 k==1 ,就把 bitmap[0]=1；如果 k==n,把 bitmap[n-1] =1；

最后只要从 bitmap 的零位一直遍历到最后，然后提取出对应为1的下标整数k，再转换成ip地址，就完成了从小到大的排序。空间复杂度很小，时间复杂度O（n）

数组中出现次数超过一半的数字

剑指 Offer 39 题

数组中有一个数字出现的次数超过数组长度的一半，请找出这个数字。

可以假设数组是非空的，并且给定的数组总是存在多数元素。

示例 1:

输入: [1, 2, 3, 2, 2, 2, 5, 4, 2]
输出: 2

解题思路

数组中有一个数字出现的次数超过数组长度的一半，也就是说它出现的次数比其他所有数字出现次数的和还要多。因此可以考虑在遍历数组的时候保存两个值：一个是数组中的一个数字，一个是次数。当我们遍历到下一个数字的时候，如果下一个数字和我们之前保存的数字相同，则次数加1；如果下一个数字和我们之前保存的数字不同，则次数减1。如果次数为零，我们需要保存下一个数字，并把次数设为1。由于我们要找的数字出现的次数比其他所有数字出现的次数之和还要多，那么要找的数字肯定是最后一次把次数设为 1 时对应的数字。

代码实现

func majorityElement(nums []int) int {
    if len(nums) == 0 {
        return 0
    }
    ret := nums[0]
    count := 1
    for i := 1; i < len(nums); i++ {
        if count == 0 {
            ret = nums[i]
            count = 1
            continue
        }
        if nums[i] == ret {
            count++
            continue
        }
        count--
    }
    return ret
}

二维数组查找

题目描述：

在一个二维数组中，每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

问题解析：
这一道题还是比较简单的，我们需要考虑的是如何做，效率最快。这里有一种很好理解的思路：

矩阵是有序的，从左下角来看，向上数字递减，向右数字递增， 因此从左下角开始查找，当要查找数字比左下角数字大时，右移；要查找数字比左下角数字小时，上移。这样找的速度最快。

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int row = matrix.length-1;//行数
        int column = 0;//列数
        
        //边界条件
        while(row>=0 && column<matrix[0].length) {
            if(matrix[row][column] > target) {
                row--;
            } else if(matrix[row][column] < target) {
                column ++;
            } else {
                return true;
            }
        }
        return false;
    }
}

go 版本：

func findNumberIn2DArray(matrix [][]int, target int) bool {
    rowNum := len(matrix)
    if rowNum == 0 {
        return false
    }

    lieNum := len(matrix[0])
    i := rowNum - 1
    j := 0
    for i >= 0 && j < lieNum {
        if matrix[i][j] == target {
            return true
        }
        if matrix[i][j] > target {
            i--
        } else {
            j++
        }
    }
    return false
}

按奇偶排序数组

剑指 offer 第 21 题：

输入一个整数数组，实现一个函数来调整该数组中数字的顺序，使得所有奇数在数组的前半部分，所有偶数在数组的后半部分。

示例：

输入：nums = [1,2,3,4]
输出：[1,3,2,4]
注：[3,1,2,4] 也是正确的答案之一。

实现思路

这个题目要求把奇数放在数组的前半部分，偶数放在数组的后半部分，因此所有的奇数应该位于偶数的前面。

也就是说我们在扫描这个数组的时候，如果发现有偶数出现在奇数的前面，我们可以交换它们的顺序，交换之后就符合要求了。

因此我们可以维护两个指针，第一个指针初始化时指向数组的第一个数字，它只向后移动；第二个指针初始化时指向数组的最后一个数字，它只向前移动。在两个指针相遇之前，第一个指针总是位于第二个指针的前面。如果第一个指针指向的数字是偶数，并且第二个指针指向的数字是奇数，我们就交换这两个数字。

代码实现

func exchange(nums []int) []int {
    pHead := 0
    pEnd := len(nums)-1
    for pEnd>pHead {
        if nums[pHead] & 1 == 1{
            pHead++
        } else {
            nums[pHead],nums[pEnd] = nums[pEnd],nums[pHead]
            pEnd--
        }
    }
    return nums
}

类似的题目还有：

给定一个非负整数数组 A，返回一个数组，在该数组中， A 的所有偶数元素之后跟着所有奇数元素。

（很早之前做的题目，用的 JAVA）

class Solution {
    public int[] sortArrayByParity(int[] A) {
        int len = A.length;
        if(len == 0 || len ==1) {
            return A;
        }
        int[] arrays = new int[len];
        int count = 0;//用来计算偶数个数
        int index = 0;//用来指明当前到达那个位置

        //先统计偶数个数
        for(int i=0;i<len;i++) {
            if(A[i]%2 == 0) {
                count++;
            }
        }
        //奇数只在插在偶数个数之后的位置
        for(int i=0;i<len;i++) {
            if(A[i]%2 == 0) {
                arrays[index++] = A[i];
            } else {
                arrays[count++] = A[i];
            }
        }
        return arrays;
    }
}

旋转数组

剑指 offer 第 11 题，leetcode 154 题

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。

给你一个可能存在重复元素值的数组 numbers ，它原来是一个升序排列的数组，并按上述情形进行了一次旋转。请返回旋转数组的最小元素。例如，数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一次旋转，该数组的最小值为 1。

注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。

示例 1：

输入：numbers = [3,4,5,1,2]
输出：1

示例 2：

输入：numbers = [2,2,2,0,1]
输出：0

实现思路

这道题最简单的方式就是直接遍历数组，找到最小的数返回，但这不是最优解，更好的方式是采用二分查找。

用两个指针分别指向数组的第一个元素和最后一个元素。按照题目中旋转的规则，第一个元素应该是大于或者等于最后一个元素的（这其实不完全对，还有特例，后面再加以讨论）。

接着可以找到数组中间的元素。如果该中间元素位于前面的递增子数组，那么它应该大于或者等于第一个指针指向的元素。此时数组中最小的元素应该位于该中间元素的后面。我们可以把第一个指针指向该中间元素，这样可以缩小寻找的范围。移动之后的第一个指针仍然位于前面的递增子数组之中。

同样，如果中间元素位于后面的递增子数组，那么它应该小于或者等于第二个指针指向的元素。此时该数组中最小的元素应该位于该中间元素的前面。我们可以把第二个指针指向该中间元素，这样也可以缩小寻找的范围。移动之后的第二个指针仍然位于后面的递增子数组之中。

不管是移动第一个指针还是第二个指针，查找范围都会缩小到原来的一半。接下来我们再用更新之后的两个指针，重复做新一轮的查找。按照上述的思路，第一个指针总是指向前面递增数组的元素，而第二个指针总是指向后面递增数组的元素。最终第一个指针将指向前面子数组的最后一个元素，而第二个指针会指向后面子数组的第一个元素。也就是它们最终会指向两个相邻的元素，而第二个指针指向的刚好是最小的元素。这就是循环结束的条件。

以前面的数组{3, 4, 5, 1, 2}为例，先把第一个指针指向第0个元素，把第二个指针指向第4个元素，位于两个指针中间（在数组中的下标是 2）的数字是 5，它大于第一个指针指向的数字。因此中间数字5一定位于第一个递增子数组中，并且最小的数字一定位于它的后面。因此我们可以移动第一个指针让它指向数组的中间。此时位于这两个指针中间（在数组中的下标是3）的数字是1，它小于第二个指针指向的数字。因此这个中间数字 1 一定位于第二个递增字数组中，并且最小的数字一定位于它的前面或者它自己就是最小的数字。因此我们可以移动第二个指针指向两个指针中间的元素即下标为 3 的元素。

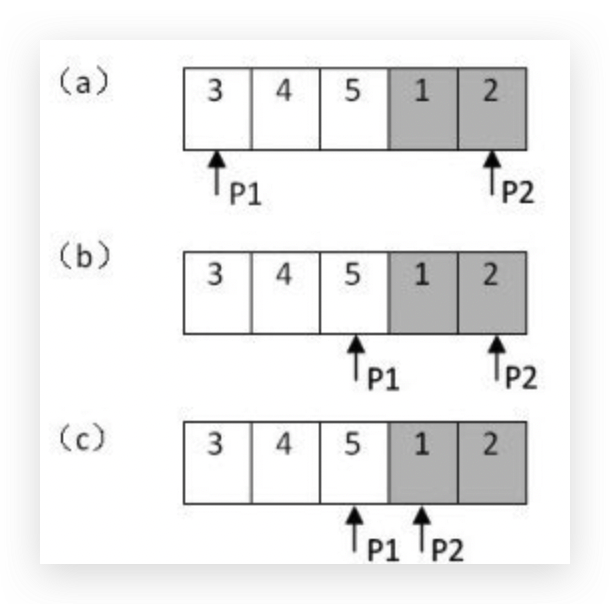
再来看一个例子。数组{1,0,1,1,1}和数组{1,1,1,0,1}都可以看成是递增排序数组{0,1,1,1,1}的旋转，在这两个数组中，第一个数字、最后一个数字和中间数字都是1，我们无法确定中间的数字 1 属于第一个递增子数组还是属于第二个递增子数组

在这两种情况中，第一个指针和第二个指针指向的数字都是1，并且两个指针中间的数字也是1，这3个数字相同。在第一种情况中，中间数字（下标为2）位于后面的子数组；在第二种情况中，中间数字（下标为2）位于前面的子数组中。因此，当两个指针指向的数字及它们中间的数字三者相同的时候，我们无法判断中间的数字是位于前面的子数组中还是后面的子数组中，也就无法移动两个指针来缩小查找的范围。

但是，由于他们的值相同，此时可以忽略掉一个，让 p1 往前挪一位或者 p2 往后挪一位。

代码实现

func minArray(numbers []int) int {
    low := 0
    high := len(numbers) - 1
    for low < high {
        pivot := low + (high - low) / 2
        if numbers[pivot] < numbers[high] {
            high = pivot
        } else if numbers[pivot] > numbers[high] {
            low = pivot + 1
        } else {
            high--
        }
    }
    return numbers[low]
}

顺时针打印矩阵

Leetcode:输入一个矩阵，按照从外向里以顺时针的顺序依次打印出每一个数字。

示例 1：

输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

示例 2：

输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]

解题思路

1. 空值处理： 当 matrix 为空时，直接返回空列表 [] 即可。
2. 初始化： 矩阵 左、右、上、下 四个边界 l , r , t , b ，用于打印的结果列表 res 。
3. 循环打印： “从左向右、从上向下、从右向左、从下向上” 四个方向循环，每个方向打印中做以下三件事 （各方向的具体信息见下表） ；

• 根据边界打印，即将元素按顺序添加至列表 res 尾部；
• 边界向内收缩 1 （代表已被打印）；
• 判断是否打印完毕（边界是否相遇），若打印完毕则跳出。

4. 返回值： 返回 res 即可。

打印方向	1. 根据边界打印	2. 边界向内收缩	3. 是否打印完毕
从左向右	左边界 l ，右边界 r	上边界 t 加 1	是否 t > b
从上向下	上边界 t ，下边界 b	右边界 r 减 1	是否 l > r
从右向左	右边界 r ，左边界 l	下边界 b 减 1	是否 t > b
从下向上	下边界 b ，上边界 t	左边界 l 加 1	是否 l > r

package com.xm.algorithm;

public class SpiralOrder {
    public int[] spiralOrder(int[][] matrix) {
        if(matrix.length == 0 || matrix == null) {
            return new int[0];
        }
        //左边界
        int l = 0;
        //右边界
        int r = matrix[0].length-1;
        //上边界
        int t = 0;
        //下边界
        int b = matrix.length-1;
        //输出结果集
        int[] result = new int[(r+1) * (b+1)];
        int x = 0;

        while(true) {
            //从左到右遍历
            for (int i = l; i <= r; i++) {
                result[x++] = matrix[t][i];
            }
            if(++t > b) {
                break;
            }
            //从上到下遍历
            for (int i = t; i <= b; i++) {
                result[x++] = matrix[i][r];
            }
            if(--r < l) {
                break;
            }
            //从右往左遍历
            for (int i = r; i >= l; i--) {
                result[x++] = matrix[b][i];
            }
            if(--b < t) {
                break;
            }
            //从下往上遍历
            for (int i = b; i >= t; i--) {
                result[x++] = matrix[i][l];
            }
            if(++l > r) {
                break;
            }
        }
        return result;
    }
}

go 解法：

func spiralOrder(matrix [][]int) []int {
    var ret []int
    row := len(matrix) // 行数
    if row == 0 {
        return nil
    }
    column := len(matrix[0]) // 列数
    if column == 0 {
        return nil
    }

    rs := 0
    re := column - 1 
    cs := 0
    ce := row - 1 
    for re >= rs && ce >= cs {
        oneSpiral := spiralOnce(matrix, rs, re, cs, ce)
        ret = append(ret, oneSpiral...)
        rs++
        re--
        cs++
        ce--
    }
    return ret
}

func spiralOnce(matrix [][]int, rs, re, cs, ce int) []int {
    var ret []int
    for r := rs; r <= re; r++ {
        ret = append(ret, matrix[cs][r])
    }
    for c := cs + 1; c <= ce; c++ {
        ret = append(ret, matrix[c][re])
    }

  // 判断是否最后一圈，最后一圈不用再遍历这里，不然会多遍历数据
    if rs < re && cs < ce {
        for r := re - 1; r >= rs; r-- {
            ret = append(ret, matrix[ce][r])
        }
        for c := ce - 1; c > cs; c-- {
            ret = append(ret, matrix[c][rs])
        }
    }
    return ret
}

复杂度分析：

• 时间复杂度 O(MN) ： M,N 分别为矩阵行数和列数。
• 空间复杂度 O(1) ： 四个边界 l , r , t , b 使用常数大小的额外空间（ res 为必须使用的空间）。

矩阵中的路径

剑指 offer 12 题

请设计一个函数，用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一格开始，每一步可以在矩阵中向左、右、上、下移动一格。如果一条路径经过了矩阵的某一格，那么该路径不能再次进入该格子。例如，在下面的3×4的矩阵中包含一条字符串“bfce”的路径（路径中的字母用加粗标出）。

[["a","b","c","e"],
["s","f","c","s"],
["a","d","e","e"]]

但矩阵中不包含字符串“abfb”的路径，因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后，路径不能再次进入这个格子。

示例 1：

输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出：true

示例 2：

输入：board = [["a","b"],["c","d"]], word = "abcd"
输出：false

解题思路

本问题是典型的矩阵搜索问题，可使用 深度优先搜索（DFS）+ 剪枝 解决。

算法原理：

• 深度优先搜索： 可以理解为暴力法遍历矩阵中所有字符串可能性。DFS 通过递归，先朝一个方向搜到底，再回溯至上个节点，沿另一个方向搜索，以此类推。
• 剪枝： 在搜索中，遇到 这条路不可能和目标字符串匹配成功 的情况（例如：此矩阵元素和目标字符不同、此元素已被访问），则应立即返回，称之为 可行性剪枝 。

算法剖析：

• 递归参数： 当前元素在矩阵 board 中的行列索引 i 和 j ，当前目标字符在 word 中的索引 k 。

• 终止条件：

  1. 返回 false：

     ① 行或列索引越界 或 ② 当前矩阵元素与目标字符不同 或 ③ 当前矩阵元素已访问过 （③ 可合并至 ② ） 。

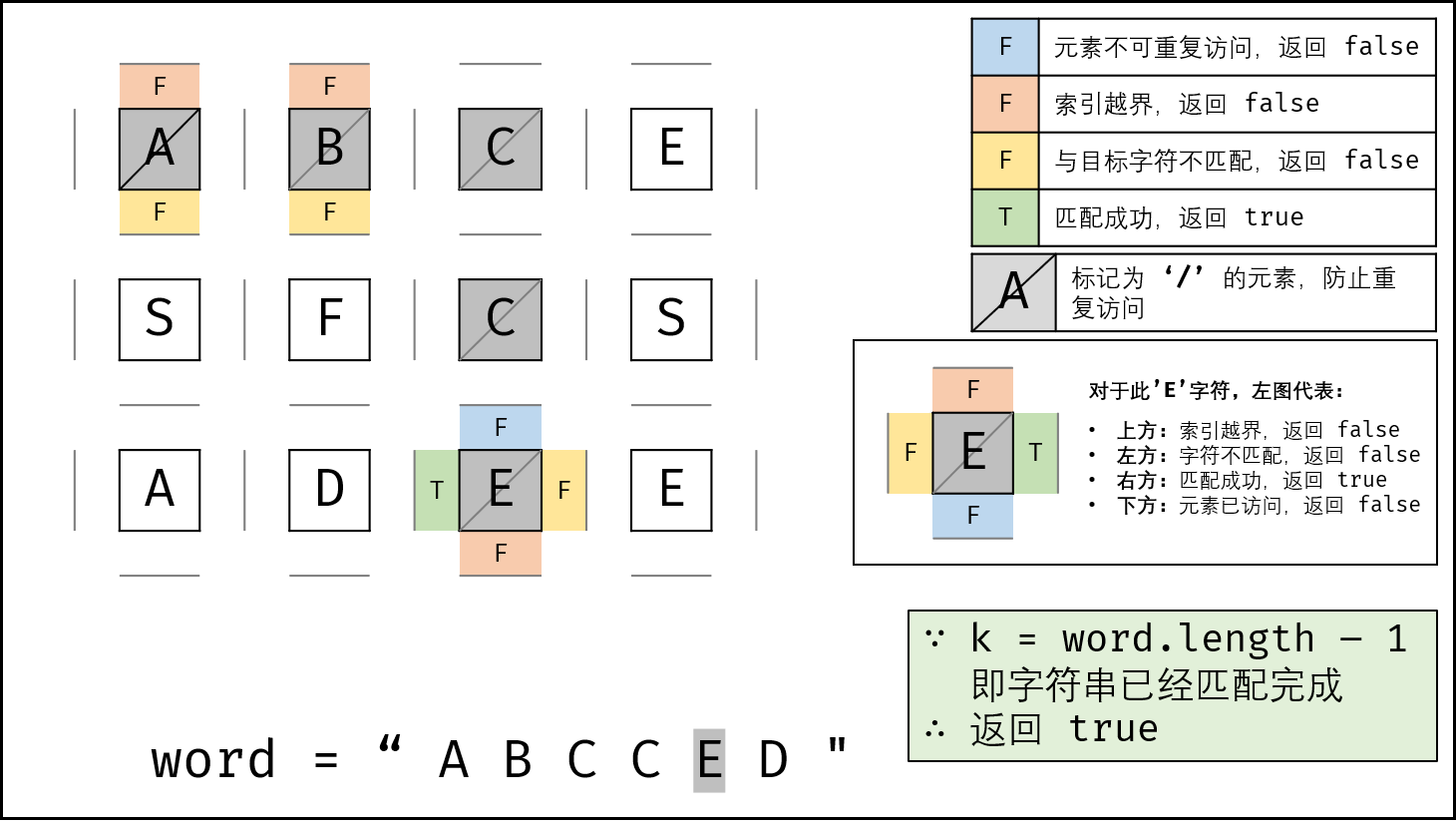
  2. 返回 true ： 字符串 word 已全部匹配，即 k = len(word) - 1 。

• 递推工作：

  1. 标记当前矩阵元素： 将 board[i][j] 值暂存于变量 tmp ，并修改为字符 '/' ，代表此元素已访问过，防止之后搜索时重复访问。
  2. 搜索下一单元格： 朝当前元素的 上、下、左、右 四个方向开启下层递归，使用 或 连接 （代表只需一条可行路径） ，并记录结果至 res 。
  3. 还原当前矩阵元素： 将 tmp 暂存值还原至 board[i][j] 元素。

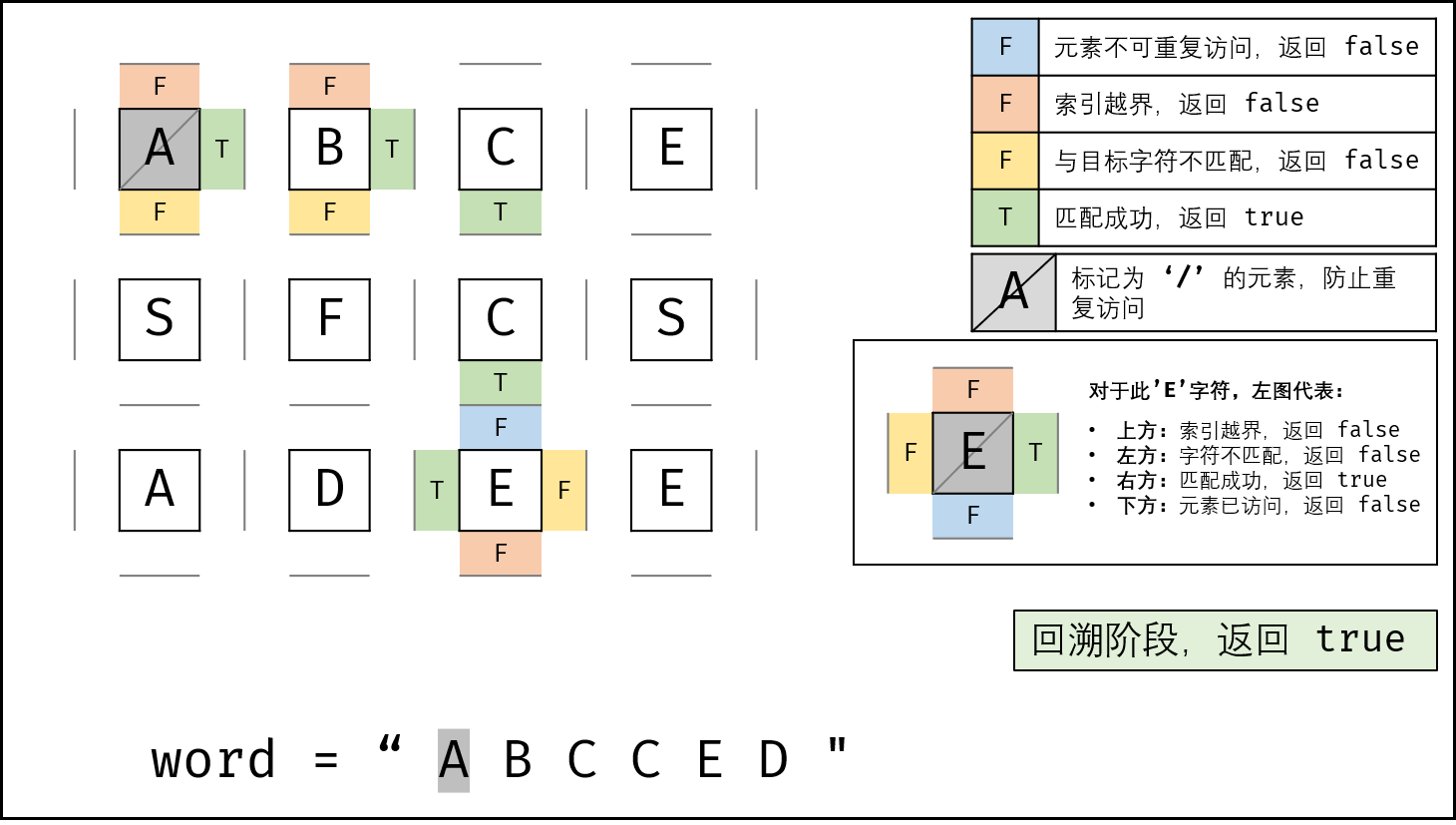
• 回溯返回值： 返回 res ，代表是否搜索到目标字符串。

代码实现

public class WordSearchInMatrix {
    public boolean exist(char[][] board, String word) {
        char[] words = word.toCharArray();
        // 这里遍历了任意开始的位置
        for (int i = 0; i < board.length; i++) {
            for (int j = 0; j < board[0].length; j++) {
                if (bfs(board, words, i, j, 0)) {
                    return true;
                }
            }
        }
        return false;
    }

    public boolean bfs(char[][] board, char[] words, int i, int j, int k) {
        //判断下标是否越界，值是否相等
        if (i < 0 || i >= board.length || j < 0 || j >= board[0].length
                || board[i][j] != words[k]) {
            return false;
        }
        if (k == words.length - 1) {
            return true;
        }
        char temp = board[i][j];
        board[i][j] = '/';
        //深度递归遍历（顺序为下、上、右、左）
        boolean res = bfs(board, words, i + 1, j, k + 1) || bfs(board, words, i - 1, j, k + 1)
                || bfs(board, words, i, j + 1, k + 1) || bfs(board, words, i, j - 1, k + 1);
        board[i][j] = temp;
        return res;
    }
}

替换空格

剑指offer：请实现一个函数，将一个字符串中的每个空格替换成%20。例如，当字符串为We Are Happy.则经过替换之后的字符串为We%20Are%20Happy。

public class ReplaceSpaceSolution {

    //方法一：循环遍历替换
    public static String replaceSpace(String str) {
        int len = str.length();
        StringBuilder result = new StringBuilder();
        for (int i = 0; i < len; i++) {
            char c = str.charAt(i);
            if(String.valueOf(c).equals(" ")) {
                result.append("%20");
            } else {
                result.append(c);
            }
        }
        return result.toString();
    }

    //方法二：使用接口
    public static String replaceSpace2(String str) {
        return str.replaceAll(" ","%20");
    }
}

最长公共前缀

Leetcode: 编写一个函数来查找字符串数组中的最长公共前缀。如果不存在公共前缀，返回空字符串 “”。

方法1:

public static  String longestCommonPrefix(String[] strs){

    if(strs.length == 0) return "";
    String prefix = strs[0];//以第一个字符串先假设为最长前缀
    int len = strs.length;
    for (int i = 1; i < len; i++) {
        //indexOf在找不到的时候返回-1，找到了返回位置
        while (strs[i].indexOf(prefix) != 0) {
            //找不到或者找到的位置不是首位，将前缀去掉一个字符再比较
            prefix = prefix.substring(0, prefix.length() - 1);
            if (prefix.isEmpty()) return "";
        }
    }
    return prefix;
}

方法2:

public static String longestCommonPrefix2(String[] strs) {
    //将首个字符串逐列与后面的字符串比较
    if(strs == null || strs.length == 0) return "";
    for (int i = 0; i < strs[0].length(); i++) {
        char c = strs[0].charAt(i);
        for (int j = 1; j < strs.length; j++) {
            if(i == strs[j].length() || c != strs[j].charAt(i)) {
                return strs[0].substring(0,i);
            }
        }
    }
    return strs[0];
}

方法3:

public static String longestCommonPrefix3(String[] strs) {
    // 先利用Arrays.sort(strs)为数组排序，
    // 排序后公共的前缀如果有，第一和最后一个肯定都包括了
    // 再将数组第一个元素和最后一个元素的字符从前往后对比

    //如果检查值不合法就返回空串
    if(!checkStr(strs)) {
        return "";
    }
    int len = strs.length;
    StringBuffer result = new StringBuffer();
    Arrays.sort(strs);
    int m = strs[0].length();
    int n = strs[len-1].length();
    int num = Math.min(m,n);
    for (int i = 0; i < num; i++) {
        if(strs[0].charAt(i) == strs[len-1].charAt(i)) {
            result.append(strs[0].charAt(i));
        } else
            break;
    }
    return result.toString();
}

private static boolean checkStr(String[] strs) {
    boolean flag = false;
    if(strs != null) {
        //遍历strs检查元素值
        for (int i = 0; i < strs.length; i++) {
            if(strs[i] != null && strs[i].length() != 0) {
                flag = true;
            } else {
                flag = false;
                break;
            }
        }
    }
    return flag;
}

最长回文串

LeetCode: 给定一个包含大写字母和小写字母的字符串，找到通过这些字母构造成的最长的回文串。在构造过程中，请注意区分大小写。比如”Aa”不能当做一个回文字符串。注 意:假设字符串的长度不会超过 1010。

回文串：“回文串”是一个正读和反读都一样的字符串，比如“level”或者“noon”等等就是回文串。——百度百科

构成回文串的两种情况：

• 字符出现次数为双数的组合
• 字符出现次数为双数的组合+一个只出现一次的字符

统计字符出现的次数即可，双数才能构成回文。因为允许中间一个数单独出现，比如“abcba”，所以如果最后有字母落单，总长度可以加 1。首先将字符串转变为字符数组。然后遍历该数组，判断对应字符是否在 hashset 中，如果不在就加进去，如果在就让 count++，然后移除该字符,这样就能找到出现次数为双数的字符个数。

class Solution {
    public int longestPalindrome(String s) {
        HashSet<Character> set = new HashSet<>();
        int len = s.length();
        int count = 0;
        // char[] chars = s.toCharArray(); //可以考虑先将字符串转化为字符数组
        for(int i=0;i<len;i++){
            char c = s.charAt(i);
            if(!set.contains(c)) {
                //如果集合里不存在就将其加入到集合
                set.add(c);
            } else {
                //如果集合里已经有了，那么就将该元素删除
                //count+1表示双数的字符个数
                set.remove(c);
                count++;
            }
        }
        //如果集合不为空，可以有一个作为最中间元素
        return set.isEmpty()?count*2:count*2+1;
    }
}

验证回文串

LeetCode: 给定一个字符串，验证它是否是回文串，只考虑字母和数字字符，可以忽略字母的大小写。 说明：本题中，我们将空字符串定义为有效的回文串。

输入: "A man, a plan, a canal: Panama"
输出: true

class Solution {
    public boolean isPalindrome(String s) {
        int len = s.length();
        if (len == 0) return true;

        int l = 0;
        int r = len-1;
        //从两边往中间遍历
        while(l< r) {
            char left = s.charAt(l);
            char right = s.charAt(r);
            //排除不是数字和字母的字符
            if(!Character.isLetterOrDigit(left)){
                l++;
            } else if(!Character.isLetterOrDigit(right)) {
                r--;
            } else {
                if( Character.toLowerCase(left) != Character.toLowerCase(right)) {
                    return false;
                }
                l++;
                r--;
            }
        }
        return true;
    }
}

最长回文子串

Leetcode: LeetCode: 最长回文子串 给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为1000。

示例 1：

输入: "babad"
输出: "bab"
注意: "aba"也是一个有效答案。

示例 2：

输入: "cbbd"
输出: "bb"

思路：遍历，以某个元素为中心，分别计算偶数长度的回文最大长度和奇数长度的回文最大长度

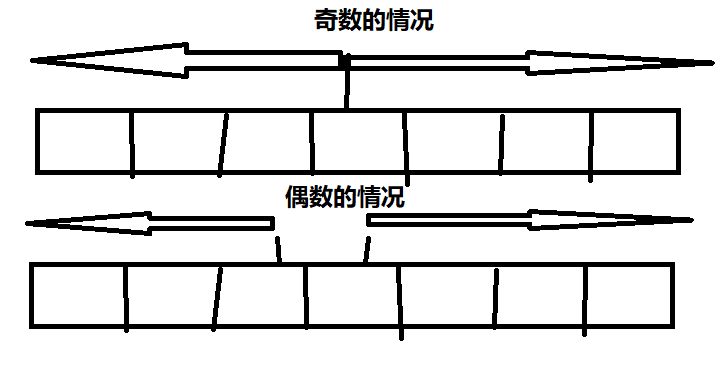
class Solution {
    private int len;//用于确定最长回文子串长度
    private int index;//用于指定从哪里开始

    public String longestPalindrome(String s) {
        int length = s.length();
        
        if(length < 2) {
            return s;
        }
        for(int i = 0;i<length-1;i++){
            //对单数检索
            palindromeHelper(s,i,i);
            //对双数检索
            palindromeHelper(s,i,i+1);
        }
        return s.substring(index,index+len);
    }

    public void palindromeHelper(String s,int l,int r) {
        int length = s.length();
        //分别往左，往右对比
        while(l >= 0 && r < length && s.charAt(l) == s.charAt(r)) {
            l--;
            r++;
        }
        //如果长度比已经对比过的长，则进行替换
        if(len < r-l-1) {
            index = l+1;//因为l位置已经不同，所以起始位置是l+1
            len = r-l-1;
        }
    }
}

最长回文子序列

LeetCode: 最长回文子序列 给定一个字符串s，找到其中最长的回文子序列。可以假设s的最大长度为1000。

最长回文子序列和上一题最长回文子串的区别是，子串是字符串中连续的一个序列，而子序列是字符串中保持相对位置的字符序列，例如，”bbbb”可以是字符串”bbbab”的子序列但不是子串。

解题思路：主要运用动态规划的思想

• 状态：f[i][j] 表示 s 的第 i 个字符到第 j 个字符组成的子串中，最长的回文序列长度是多少。
• 转移方程：如果 s 第 i 个字符和第 j 个字符相同的话 f[i][j] = f[i + 1][j - 1] + 2;否则 f[i][j] = max(f[i + 1][j], f[i][j - 1])
• 初始化：f[i][i] = 1 单个字符的最长回文序列是1
• 结果：f[0][n-1]

class Solution {
    public int longestPalindromeSubseq(String s) {
        int len = s.length();
        int[][] result = new int[len][len];
        for(int i = len-1;i >= 0;i--) {
            //单个字符长度为1
            result[i][i] = 1;
            for(int j=i+1;j<len;j++) {
                if(s.charAt(i) == s.charAt(j)) {
                    //如果相同，则在原来序列数量的左右两边各加一个，所以加2
                    result[i][j] = result[i+1][j-1] +2;
                } else {
                    //如果不相同，则是当前位置到上一个位置的值，这个值可能是i这边，也可能是j一边的，取最大值。
                    result[i][j] = Math.max(result[i+1][j],result[i][j-1]);
                }
            }
        }
        return result[0][len-1];
    }
}

括号匹配深度

输入描述:
输入包括一个合法的括号序列s,s长度length(2 ≤ length ≤ 50),序列中只包含'('和')'。

输出描述:
输出一个正整数,即这个序列的深度。

示例：

输入:
(())
输出:
2

package com.xm.algorithm;

import java.util.Scanner;

public class BracketMatchingDepth {

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        String s = scanner.nextLine();
        int i = maxDepth(s);
        System.out.println("最大深度为："+i);
        scanner.close();
    }

    public static int maxDepth(String s) {
        int len = s.length();
        int count = 0;
        int depth = 0;
        for(int i=0;i<len;i++) {
            switch (s.charAt(i)) {
                case '(':count++ ;
                    break;
                case ')':count--;
                    break;
            }
            //关键在这里需要记录下当前匹配的最大深度
            depth = Math.max(count, depth);
        }
        return depth;
    }
}

把数字字符串转换成整数

剑指offer: 将一个字符串转换成一个整数(实现Integer.valueOf(string)的功能，但是string不符合数字要求时返回0)，要求不能使用字符串转换整数的库函数。 数值为0或者字符串不是一个合法的数值则返回0。

package com.xm.algorithm;


public class StrToInt {

    public static void main(String[] args) {
        String s = "-12312312";
        System.out.println("使用库函数转换：" + Integer.valueOf(s));
        int res = strToInt(s);
        System.out.println("使用自己写的方法转换：" + res);
    }

    public static int strToInt(String str) {
        int len = str.length();
        int result = 0;
        char[] chars = str.toCharArray();
        int flag = 0;//用于判断是否有符号位
        if(chars[0] == '+')
            flag = 1;
        else if(chars[0] == '-')
            flag = 2;
        //判断从哪一位开始，有符号就从第二个开始
        int start = (flag == 0) ? 0 : 1;
        for (int i = start;i<len;i++) {
            if(Character.isDigit(chars[i])) {
                int temp = chars[i] - '0';
                result = result*10+temp;
            } else {
                return 0;
            }
        }
        return (flag==2)? -result : result;
    }
}

最长不重复子串

LeeCode：给定一个字符串，请你找出其中不含有重复字符的最长子串的长度。

思路：采用窗口滑动思想，利用 HashMap，其中 key 存储字符，value 存储当前字符的下一个位置。窗口（i，j）从左往右扫描，当 key 不重复时，j+1，继续往右扫描；当出现 key 重复时，i 跳过 key 字符第一次出现的位置到它的下一个位置，而长度就是 j-i+1 的长度。

public  int lengthOfLongestSubstring03(String s) {
    int n = s.length(), ans = 0;
    //创建map窗口,i为左区间，j为右区间，右边界移动
    Map<Character, Integer> map = new HashMap<>();
    for (int j = 0, i = 0; j < n; j++) {
        // 如果窗口中包含当前字符，
        if (map.containsKey(s.charAt(j))) {
            //左边界移动到 相同字符的下一个位置和i当前位置中更靠右的位置，这样是为了防止i向左移动
            i = Math.max(map.get(s.charAt(j)), i);
        }
        //比对当前无重复字段长度和储存的长度，选最大值并替换
        //j-i+1是因为此时i,j索引仍处于不重复的位置，j还没有向后移动，取的[i,j]长度
        ans = Math.max(ans, j - i + 1);
        // 将当前字符为key，下一个索引为value放入map中
        // value为j+1是为了当出现重复字符时，i直接跳到上个相同字符的下一个位置，if中取值就不用+1了
        map.put(s.charAt(j), j+1);
    }
    return ans;
}

两个字符串A,B，将所有同时存在于A,B中的字母从A中剔除

public class Solution {

    public static String solution(String a,String b) {
        HashSet<Character> set = new HashSet<>();
        StringBuilder builder = new StringBuilder();
        for (int i = 0; i < b.length(); i++) {
            set.add(b.charAt(i));
        }
        for (int i = 0; i < a.length(); i++) {
            char c = a.charAt(i);
            if(!set.contains(c)) {
                builder.append(c);
            }
        }
        return builder.toString();
    }
}

字符串转整数

Leetcode 第 8 题

请实现一个 myAtoi(string s) 函数，使其能将字符串转换成一个 32 位有符号整数（类似 C/C++ 中的 atoi 函数）。

函数 myAtoi(string s) 的算法如下：

1. 读入字符串并丢弃无用的前导空格
2. 检查下一个字符（假设还未到字符末尾）为正还是负号，读取该字符（如果有）。 确定最终结果是负数还是正数。 如果两者都不存在，则假定结果为正。
3. 读入下一个字符，直到到达下一个非数字字符或到达输入的结尾。字符串的其余部分将被忽略。
   将前面步骤读入的这些数字转换为整数（即，”123” -> 123， “0032” -> 32）。如果没有读入数字，则整数为 0 。必要时更改符号（从步骤 2 开始）。
4. 如果整数数超过 32 位有符号整数范围 [−231, 231 − 1] ，需要截断这个整数，使其保持在这个范围内。具体来说，小于 −231 的整数应该被固定为 −231 ，大于 231 − 1 的整数应该被固定为 231 − 1 。
5. 返回整数作为最终结果。

注意：本题中的空白字符只包括空格字符 ‘ ‘ 。除前导空格或数字后的其余字符串外，请勿忽略任何其他字符。

示例 1：

输入：s = "42"
输出：42
解释：加粗的字符串为已经读入的字符，插入符号是当前读取的字符。
第 1 步："42"（当前没有读入字符，因为没有前导空格）
         ^
第 2 步："42"（当前没有读入字符，因为这里不存在 '-' 或者 '+'）
         ^
第 3 步："42"（读入 "42"）
           ^
解析得到整数 42 。
由于 "42" 在范围 [-231, 231 - 1] 内，最终结果为 42 。

示例 2：

输入：s = "   -42"
输出：-42
解释：
第 1 步："   -42"（读入前导空格，但忽视掉）
            ^
第 2 步："   -42"（读入 '-' 字符，所以结果应该是负数）
             ^
第 3 步："   -42"（读入 "42"）
               ^
解析得到整数 -42 。
由于 "-42" 在范围 [-231, 231 - 1] 内，最终结果为 -42 。

示例 3：

输入：s = "4193 with words"
输出：4193
解释：
第 1 步："4193 with words"（当前没有读入字符，因为没有前导空格）
         ^
第 2 步："4193 with words"（当前没有读入字符，因为这里不存在 '-' 或者 '+'）
         ^
第 3 步："4193 with words"（读入 "4193"；由于下一个字符不是一个数字，所以读入停止）
             ^
解析得到整数 4193 。
由于 "4193" 在范围 [-231, 231 - 1] 内，最终结果为 4193 。

示例 4：

输入：s = "words and 987"
输出：0
解释：
第 1 步："words and 987"（当前没有读入字符，因为没有前导空格）
         ^
第 2 步："words and 987"（当前没有读入字符，因为这里不存在 '-' 或者 '+'）
         ^
第 3 步："words and 987"（由于当前字符 'w' 不是一个数字，所以读入停止）
         ^
解析得到整数 0 ，因为没有读入任何数字。
由于 0 在范围 [-231, 231 - 1] 内，最终结果为 0 。

示例 5：

输入：s = "-91283472332"
输出：-2147483648
解释：
第 1 步："-91283472332"（当前没有读入字符，因为没有前导空格）
         ^
第 2 步："-91283472332"（读入 '-' 字符，所以结果应该是负数）
          ^
第 3 步："-91283472332"（读入 "91283472332"）
                     ^
解析得到整数 -91283472332 。
由于 -91283472332 小于范围 [-231, 231 - 1] 的下界，最终结果被截断为 -231 = -2147483648 。

解题思路

本题有两种解题思路，第一种比较直接，就是挨个字符进行判断，需要考虑各种边界条件。

比较简洁的方法是使用自动状态机的方式，本题可以建立如下的状态机：

也可以用下面的表格来表示这个自动机：

	‘’	+/-	number	other
start	start	signed	in_number	end
signed	end	end	in_number	end
in_number	end	end	in_number	end
end	end	end	end	end

接下来编程部分就非常简单了：只需要把上面这个状态转换表抄进代码即可。

另外自动机也需要记录当前已经输入的数字，只要在 s’ 为 in_number 时，更新输入的数字，即可最终得到输入的数字。

代码实现

方法一：考虑各种边界的解法

func myAtoi(s string) int {
    var (
        ret         int32 // 结果
        isNegative  bool  // 是否负数
        signed      bool  // 是否已经出现过'+'，'-'
        isStartZero bool  // 是否0开头，再出现'-'，'+'，return 0
    )
    s = strings.TrimSpace(s)

    for _, v := range s {
        // 如果是以0开头并且是第一个数字，还要满足前面没有正负符号，比如 000+100 这种就不行
        if v == '0' && ret == 0 && !signed {
            isStartZero = true
            continue
        }
        // 0 开头再出现正负，直接返回
        if isStartZero && (v == '+' || v == '-') {
            break
        }
        // 第一次出现正负符号，标记，下次再出现就 break
        if v == '+' && !signed {
            signed = true
            continue
        }
        // 例如 "123-"
        if v == '-' && !signed && ret == 0{
            signed = true
            isNegative = true
            continue
        }
        // 不符合条件，break 掉
        if v < '0' || v > '9' {
            break
        }
        // 计算边界（ ret*10+v < int32Max || -(ret*10 -v ) > int32Min
        if isNegative {
            // 化开防止溢出
            if -ret < (math.MinInt32+(v-'0'))/10 {
                ret = math.MinInt32
                break
            }
        } else {
            if ret > (math.MaxInt32-(v-'0'))/10 {
                ret = math.MaxInt32
                break
            }
        }
        ret = ret*10 + (v - '0')
    }

    if isNegative {
        ret = -ret
    }
    return int(ret)
}

方法二：状态机解法

// Automaton 状态机解法
type Automaton struct {
    Sign   int
    Status string
    Ret    int64

    table map[string][]string // 状态表
}

func initAutomaton() Automaton {
    return Automaton{
        Sign:   1,
        Status: "start",
        Ret:    0,
        table: map[string][]string{
            "start":     {"start", "signed", "in_number", "end"},
            "signed":    {"end", "end", "in_number", "end"},
            "in_number": {"end", "end", "in_number", "end"},
            "end":       {"end", "end", "end", "end"},
        },
    }
}

func (a *Automaton) get(c uint8) {
    a.Status = a.table[a.Status][getCol(c)]
    if a.Status == "in_number" {
        a.Ret = a.Ret*10 + int64(c-'0')
        if a.Sign == 1 {
            a.Ret = min(a.Ret, math.MaxInt32)
        } else {
            a.Ret = min(a.Ret, -math.MinInt32)
        }
    } else if a.Status == "signed" {
        if c == '+' {
            a.Sign = 1
        } else {
            a.Sign = -1
        }
    }
}

func getCol(c uint8) int {
    if c == ' ' {
        return 0
    }
    if c == '+' || c == '-' {
        return 1
    }
    if c >= '0' && c <= '9' {
        return 2
    }
    return 3
}

func min(a, b int64) int64 {
    if a >= b {
        return b
    }
    return a
}

func myAtoi(s string) int {
    automaton := initAutomaton()
    for i := 0; i < len(s); i++ {
        automaton.get(s[i])
    }
    return automaton.Sign * int(automaton.Ret)
}

字符串排列

剑指Offer 28 题

输入一个字符串，打印出该字符串中字符的所有排列。

你可以以任意顺序返回这个字符串数组，但里面不能有重复元素。

示例:

输入：s = "abc"
输出：["abc","acb","bac","bca","cab","cba"]

解题思路

这道题可以通过回溯的方式来做。

将这个问题看作有 n 个排列成一行的空位，我们需要从左往右依次填入题目给定的 n 个字符，每个字符只能使用一次。首先可以想到穷举的算法，即从左往右每一个空位都依次尝试填入一个字符，看是否能填完这 n 个空位，编程实现时，可以用回溯法来模拟这个过程。

定义递归函数 recursion，当前排列为 curr，下一个待填入的空位是第 i 个空位（下标从 0 开始）。那么该递归函数分为两个情况：

1. 如果 i=n，说明我们已经填完了 n 个空位，找到了一个可行的解，我们将 curr 放入答案数组中，递归结束。
2. 如果 i<n，此时需要考虑第 i 个空位填哪个字符。根据题目要求我们肯定不能填已经填过的字符，因此很容易想到的一个处理手段是我们定义一个标记数组 visited 来标记已经填过的字符，那么在填第 i 个字符的时候我们遍历题目给定的 n 个字符，如果这个字符没有被标记过，我们就尝试填入，并将其标记，继续尝试填下一个空位，即调用函数 recursion(i+1,curr)。回溯时，我们需要要撤销该空位填的字符以及对该字符的标记，并继续向当前空位尝试填入其他没被标记过的字符。

但是该递归函数并没有满足全排列不重复的要求，在重复的字符较多的情况下，该递归函数会生成大量重复的排列。对于任意一个空位，如果存在重复的字符，该递归函数会将它们重复填上去并继续尝试导致最后答案的重复。

例如，对于字符串ab1b2b3cd，有可能会出现 ab2b1b3cd，ab3b2b1cd 这样的组合，而实际上它们都是abbbcd，这就导致了重复。

解决该问题的一种较为直观的思路是，我们首先生成所有的排列，然后进行去重。而另一种思路是我们通过修改递归函数，使得该递归函数只会生成不重复的序列。

具体地，我们只要在递归函数中设定一个规则，保证在填每一个空位的时候重复字符只会被填入一次。具体地，我们首先对原字符串排序，保证相同的字符都相邻，在递归函数中，我们限制每次填入的字符一定是这个字符所在重复字符集合中「从左往右第一个未被填入的字符」，即如下的判断条件：

isVisited || (index > 0 && sb[index-1] == sb[index] && !visited[index-1])

代码实现

func permutation(s string) []string {
    sb := []byte(s)
    sort.Slice(sb, func(i, j int) bool { return sb[i] < sb[j] })

    length := len(s)
    visited := make([]bool, length) // 标识当前位置是否已经使用
    curr := make([]byte, 0, length) // 当前排列
    var ret []string                // 返回的结果集
    var recursion func(i int)       // 递归函数
    recursion = func(i int) {
        // 填充完一个排列了
        if i == length {
            ret = append(ret, string(curr))
            return
        }
        for index, isVisited := range visited {
            // 已经被用过的不再使用
            // 当出现例如 [a,b1,b2,b3,c,d] 这种字符串时，会出现重复排列，这里需要去重，保证按照 b1b2b3 的顺序出现
            if isVisited || (index > 0 && sb[index-1] == sb[index] && !visited[index-1]) {
                continue
            }
            curr = append(curr, sb[index]) // 当前空格插入一个字符
            visited[index] = true          // 标识该字符已经被使用
            recursion(i + 1)               // 继续下一个空格的插入
            curr = curr[:len(curr)-1]      // 让出当前空格，给下一个字符（下一种排列）
            visited[index] = false         // 标识成未使用
        }
    }
    recursion(0)
    return ret
}

复杂度分析:

• 时间复杂度：O(n×n!)，其中 n 为给定字符串的长度。这些字符的全部排列有 O(n!)个，每个排列平均需要 O(n) 的时间来生成。

• 空间复杂度：O(n)，我们需要 O(n) 的栈空间进行回溯，注意返回值不计入空间复杂度。

Z 字形变换

leetcodee 第六题

将一个给定字符串 s ，根据给定的行数 numRows ，以从上往下、从左到右进行 Z 字形排列。

比如输入字符串为 “PAYPALISHIRING” 行数为 3 时，排列如下：(И字型)

P   A   H   N 
A P L S I I G
Y   I   R

之后，输出需要从左往右逐行读取，产生出一个新的字符串，比如：”PAHNAPLSIIGYIR”。

解题思路

解题的思路关键在于想到这种方式：首先构造一个长度为 numRows 的数组，在数组中来回移动放入字符串的值，这样就满足了题目要求了。

代码实现

从这道题开始，因为工作需要，改用 go 实现代码了。

import (
    "strings"
)

func convert(s string, numRows int) string {
    // 行数大直接返回整个字符串
    if len(s) <= numRows {
        return s
    }
    // 1. 初始化一个Builder数组
    resultArray := make([]strings.Builder, numRows)
    // 2. 指针在数组上来回移动赋值
    curPoint := 0
    backPoint := false
    for i := range s {
        resultArray[curPoint].WriteByte(s[i])
        // 3. 到边界时反转
        if curPoint == 0 || curPoint == numRows-1 {
            backPoint = !backPoint
        }

        // 当前所在的数组格子
        if backPoint {
            curPoint += 1
        } else {
            curPoint -= 1
        }
    }

    result := strings.Builder{}
    for i := range resultArray {
        result.WriteString(resultArray[i].String())
    }
    return result.String()
}

字符串匹配KMP算法

KMP算法是用来解决字符串查找的问题，可以在一个字符串（S）中查找一个子串（W）出现的位置。KMP 算法把字符匹配的时间复杂度缩小到O(m+n),而空间复杂度也只有O(m)。因为“暴力搜索”的方法会反复回溯主串，导致效率低下，而KMP算法可以利用已经部分匹配这个有效信息，保持主串上的指针不回溯，通过修改子串的指针，让模式串尽量地移动到有效的位置。

算法思想大概如下：

有如下字符串：

当匹配到以下这种情况时，会出现空格和D不匹配，而前面六个字符”ABCDAB”是匹配的：

此时可以将搜索项后移4格得到如下情况，然后再继续往下对比下一位：

在程序中，通过设置部分匹配表保存前面搜索的已知信息，部分匹配表主要用于保存匹配字符串的最长公共前后缀。

部分匹配值就是“前缀”和“后缀”的最长的共有元素的长度。以“ABCDABD”为例：

• “A”的前缀和后缀都为空集，共有元素的长度为0；
• “AB”的前缀为[A]，后缀为[B]，共有元素的长度为0；
• “ABC”的前缀为[A, AB]，后缀为[BC, C]，共有元素的长度0；
• “ABCD”的前缀为[A, AB, ABC]，后缀为[BCD, CD, D]，共有元素的长度为0；
• “ABCDA”的前缀为[A, AB, ABC, ABCD]，后缀为[BCDA, CDA, DA, A]，共有元素为”A”，长度为1；
• “ABCDAB”的前缀为[A, AB, ABC, ABCD, ABCDA]，后缀为[BCDAB, CDAB, DAB, AB, B]，共有元素为”AB”，长度为2；
• “ABCDABD”的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB]，后缀为[BCDABD, CDABD, DABD, ABD, BD, D]，共有元素的长度为0。

因此可以得出下表：

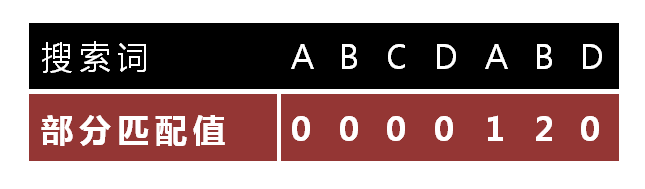
此时需要移动的位数 = 已匹配的字符数 - 对应的部分的匹配值

对于上面的情况：

查表可知，最后一个匹配字符B对应的”部分匹配值”为2，因为 6 - 2 等于4，所以将搜索词向后移动4位。

由于此时指针指向的是D位置，而并非前面的B位置，为了便于计算，可以将部分匹配值整体右移一位，之后在第0位补上值为-1。例如：

此时，若匹配到当前位置不符合，只需要将匹配位置移到当前匹配位置的匹配值代表的位置，如上面此时D的匹配值为2，则将搜索词中[2]的位置即A移到当前字符串下，同样相当于右移4位。若匹配值为-1，则从下一个位置开始从头开始匹配。

部分匹配值的实现思路

对于第一个字符，其匹配值一定是0。之后每增加一位，则与已比较的最后一位的匹配值所指位置的字符比较，相同，则在上一个字符匹配值基础上+1；如果不匹配，则需要指向最后一位字符的前一个字符的匹配值的位置的字符，之后以此类推。

/* 部分匹配表的实现
 * @pattern 需要被匹配到的字符串
 * @prefix 部分匹配表
 * @n pattern长度
 */
void prefix_table(char pattern[],int prefix[],int n) {
    prefix[0] = 0;
    int len = 0;//指向当前字符串对比到的字符的匹配值
    int i = 1;
    while(i < n) {
        if(pattern[len] == pattern[i]) {
            len++;
            prefix[i] = len;
            i++;
        } else {
            if(len > 0){
                len = prefix[len -1];
            } else {
                prefix[i] = 0;
                i++;
            }
        }
    }
}

之后再将整体匹配表的值后移一位

void move_prefix_table(int prefix[],int n) {
    int i;
    for(i = n-1;i > 0;i--) {
        prefix[i] = prefix[i-1];
    }
    prefix[0] = -1;
}

KMP算法

void kmp_search(char text[],char pattern[]) {
    int n = strlen(pattern);    //需要匹配的字符串长度
    int m = strlen(text);       //待匹配字符串长度
    int* prefix = malloc(sizeof(int)*n);
    
    //获取匹配表
    prefix_table(pattern,prefix,n);
    move_prefix_table(prefix,n);
    
    int i = 0;      //当前text匹配到的位置
    int j = 0;      //当前pattern匹配到的位置
    
    while(i < m) {
    
        //搜索完成
        if(j = n-1 && text[i] == pattern[j]) {
            printf("已找到位置：" + (i-j));
            j = prefix[j];//继续往后看看还有没有其他匹配项
        }
    
        //匹配成功
        if(text[i] == pattern[j]) {
            i++;
            j++;
        } else {
            j = prefix[j];
            //如果到了最开始还不匹配，那么往text的下一个位置从头开始匹配
            if(j == -1) {
                i++;
                j++;
            }
        }
    }
}

反转链表

剑指 offer:输入一个链表，反转链表后，输出链表的所有元素。

解题思路

这里需要用到三个指针，分别记录当前节点，当前节点的前一个节点以及当前节点的下一个节点。

代码实现

Java 版本：

package com.xm.algorithm;

import java.util.List;

public class ReverseList {

    static class ListNode {
        int data;
        ListNode next;

        ListNode(int data) {
            this.data = data;
        }
    }

    public static ListNode reverseList(ListNode head) {
        ListNode next = null;
        ListNode pre = null;

        while(head != null) {
            //记录当前节点的下一个节点
            next = head.next;
            //将当前节点的next域指向上一个节点
            head.next = pre;
            //当前节点作为“上一个节点”以供下一个节点指明
            pre = head;
            head = next;
        }
        return pre;
    }

    public static void main(String[] args) {
        ListNode a = new ListNode(1);
        ListNode b = new ListNode(2);
        ListNode c = new ListNode(3);
        ListNode d = new ListNode(4);
        ListNode e = new ListNode(5);
        a.next = b;
        b.next = c;
        c.next = d;
        d.next = e;
        reverseList(a);
        while (e != null) {
            System.out.println(e.data);
            e = e.next;
        }
    }
}

go 版本：

func reverseList(head *ListNode) *ListNode {
    var prev *ListNode
    curr := head
    for curr != nil {
        next := curr.Next
        curr.Next = prev
        prev = curr
        curr = next
    }
    return prev
}

删除链表中倒数第k个节点

Leetcode: 输入一个链表，删除该链表中倒数第k个结点，并且返回链表的头结点。

分析：

链表中倒数第 k 个节点也就是正数第 (L-K+1) 个节点，

首先两个节点/指针，一个节点 node1 先开始跑，当两者拉开距离 n 后，另一个节点 node2 开始跑，当 node1 跑到最后时，node2 所指的节点就是倒数第 k 个节点也就是正数第 (L-K+1) 个节点。

package com.xm.algorithm;

public class RemoveNthFromEnd {
    class ListNode {
        int val;
        ListNode next;

        ListNode(int val) {
            this.val = val;
        }
    }

    public ListNode removeNthFromEnd(ListNode head,int n) {
        
        ListNode dummy = new ListNode(0);
        dummy.next = head;
        ListNode node1 = dummy;
        ListNode node2 = dummy;
        
        while (node1 != null) {
            //node1先开始进入链表
            node1 = node1.next;
            //当node1与node2的距离拉开n个距离时node2开始进入链表
            if(n<1 && node1!=null){
                node2 = node2.next;
            }
            n--;
        }
        //当node1跑完时，node2的位置便是L-n，而倒数第n位的位置是L-n+1
        node2.next = node2.next.next;
        return dummy.next;
    }
}

输出链表中倒数第k个节点

题目描述:

剑指offer: 输入一个链表，输出该链表中倒数第k个结点。

问题分析

根据上一题的思路求解。

package com.xm.algorithm;

public class FindKthToTail {

    static class  ListNode {
        int val;
        ListNode next;

        ListNode(int val) {
            this.val = val;
        }
    }

    public ListNode findKthToTail(ListNode head,int n) {
        if(head == null || n<=0) {
            return null;
        }
        ListNode node1 = head;
        ListNode node2 = head;
        int count = 0;//用于计算节点个数，判断是否超出范围
        int index = n;//记录n的值，用于后面做判断

        while(node1 != null) {
            count++;
            node1 = node1.next;
            if(n<1 && node1!=null){
                node2 = node2.next;
            }
            n--;
        }
        if(count<index) {
            return null;
        }
        return node2.next;
    }
}

go 版本：

func getKthFromEnd(head *ListNode, k int) *ListNode {
    if head == nil || k <= 0 {
        return nil
    }
    
    pHead := head
    pEnd := head
    // 尾指针领先头指针 k-1
    for i := 0; i < k-1; i++ {
        pEnd = pEnd.Next
        if pEnd == nil {
            return nil
        }
    }
    for pEnd.Next != nil {
        pHead = pHead.Next
        pEnd = pEnd.Next
    }
    return pHead
}

合并两个排序的链表

剑指 offer 25 题：

输入两个递增排序的链表，合并这两个链表并使新链表中的节点仍然是递增排序的。

示例1：

输入：1->2->4, 1->3->4
输出：1->1->2->3->4->4

解题思路

首先需要判断 null，一个为 null 直接返回另外一个。然后就是每次分别把最小的节点拿出来放到新链表中，最后拼接剩余部分。

代码实现

func mergeTwoLists(l1 *ListNode, l2 *ListNode) *ListNode {
    if l1 == nil {
        return l2
    } else if l2 == nil {
        return l1
    }

    head := &ListNode{}
    curr := head // 这一步很关键

    for l1 != nil && l2 != nil {
        if l1.Val < l2.Val {
            curr.Next = l1
            l1 = l1.Next
        } else {
            curr.Next = l2
            l2 = l2.Next
        }
        curr = curr.Next
    }
  
    if l1 != nil {
        curr.Next = l1
    }else if l2 != nil {
        curr.Next = l2
    }
    return head.Next
}

如何判断单链表是否有环？如何确定环的入口？

方法一：hash 表

public class Solution {
    public boolean hasCycle(ListNode head) {
        Set<ListNode> set = new HashSet<>();
        ListNode node = head;
        while(node != null) {
            if(set.contains(node)) {
                return true;
                //对于需要返回节点的，直接返回这个node
                //即 return node;
            } else {
                set.add(node);
                node = node.next;
            }
        }
        return false;
        //这里相应改成return null;
    }
}

• 时间复杂度：O(n)，对于含有 n 个元素的链表，我们访问每个元素最多一次。添加一个结点到哈希表中只需要花费 O(1) 的时间。
• 空间复杂度：O(n)，空间取决于添加到哈希表中的元素数目，最多可以添加 n 个元素。

方法二：双指针（快慢指针）

如果存在循环，快指针会再次追上慢指针，没有说明不存在环形链表；如果需要返回入口节点，则将两个指针一个指向头节点，一个指向相遇点，然后分别向前走直到相遇，该点就是入口点。

理解如下：

1. 快指针1次走2步，慢指针1次走1步。所以快指针总是走了慢指针两倍的路。
2. 回顾一下阶段1的过程，设头节点到入环点的路途为 n, 那么慢指针走了入环路途的一半（n/2）时，快指针就到达入环点了(走完n了)。
3. 慢指针再继续走完剩下的一般入环路途（剩下的n/2），到达入环点时，快指针已经在环内又走了一个 n 那么远的路了。
4. 为了方便理解，这里先讨论环很大，大于n的情况（其他情况后文补充）。此时，慢指针正处于入环点，快指针距离入环点的距离为n。环内路，可以用此时快指针的位置分割为两段，前面的 n 部分，和后面的 b 部分。
5. 此时开始继续快慢指针跑圈，因为已经在环内了，他们其实就是在一条nbnbnbnbnbnbnb（无尽nb路）上跑步。
6. 慢指针从入环处开始跑b步，距离入环处就剩下了n。此时，快指针则是从距离入环处n步远的位置开始跑了2b步，距离入环处也是剩下了n。他们相遇了，并且距离入环处的距离就是n，n就是头节点到入环点的距离阿!!! 后面的不用说了吧。
7. 环很小的情况，其实跟环很大是一样的，比如你可以理解为将多个小环的循环铺开，虚拟扩展成一个大环来理解。

/**
 * 不需要求入口
 */
public boolean hasCycle(ListNode head) {
    if (head == null || head.next == null) {
        return false;
    }
    ListNode slow = head;
    ListNode fast = head.next;
    while (slow != fast) {
        if (fast == null || fast.next == null) {
            return false;
        }
        slow = slow.next;
        fast = fast.next.next;
    }
    return true;
}
/**
 * 求入口
 */
public class Solution {

    private ListNode getIntersect(ListNode head) {
        ListNode tortoise = head;
        ListNode hare = head;

        while (hare != null && hare.next != null) {
            tortoise = tortoise.next;
            hare = hare.next.next;
            if (tortoise == hare) {
                return tortoise;
            }
        }

        return null;
}

    public ListNode detectCycle(ListNode head) {
        if (head == null) {
            return null;
        }

        ListNode intersect = getIntersect(head);
        if (intersect == null) {
            return null;
        }

        ListNode ptr1 = head;
        ListNode ptr2 = intersect;
        while (ptr1 != ptr2) {
            ptr1 = ptr1.next;
            ptr2 = ptr2.next;
        }
        return ptr1;
    }
}

• 时间复杂度：O(n)
• 空间复杂度：O(1)，我们只使用了慢指针和快指针两个结点，所以空间复杂度为 O(1)。

找两条链表公共节点

Leecode:编写一个程序，找到两个单链表相交的起始节点。

使用双指针法：

• 创建两个指针 pA 和 pB，分别初始化为链表 A 和 B 的头结点。然后让它们向后逐结点遍历。
• 当 pA 到达链表的尾部时，将它重定位到链表 B 的头结点 (你没看错，就是链表 B); 类似的，当 pB 到达链表的尾部时，将它重定位到链表 A 的头结点。
• 若在某一时刻 pA 和 pB 相遇，则 pA/pB 为相交结点。
• 想弄清楚为什么这样可行, 可以考虑以下两个链表: A={1,3,5,7,9,11} 和 B={2,4,9,11}，相交于结点 9。 由于 B.length (=4) < A.length (=6)，pB 比 pA 少经过 2 个结点，会先到达尾部。将 pB 重定向到 A 的头结点，pA 重定向到 B 的头结点后，pB 要比 pA 多走 2 个结点。因此，它们会同时到达交点。
• 如果两个链表存在相交，它们末尾的结点必然相同。因此当 pA/Bp 到达链表结尾时，记录下链表 A/B 对应的元素。若最后元素不相同，则两个链表不相交。

复杂度分析：

• 时间复杂度 : O(m+n)O(m+n)。
• 空间复杂度 : O(1)O(1)。

public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        if (headA == null || headB == null) {
            return null;
        }
        ListNode pA = headA;
        ListNode pB = headB;
        while (pA != pB) {
            pA = pA.next;
            pB = pB.next;
            if (pA == null && pB == null) {
                return null;
            }
            if (pA == null) {
                pA = headB;
            }
            if (pB == null) {
                pB = headA;
            }
        }
        return pA;
    }
}

复杂链表的复制

剑指 Offer 第 35 题

请实现 copyRandomList 函数，复制一个复杂链表。在复杂链表中，每个节点除了有一个 next 指针指向下一个节点，还有一个 random 指针指向链表中的任意节点或者 null。

示例 1：

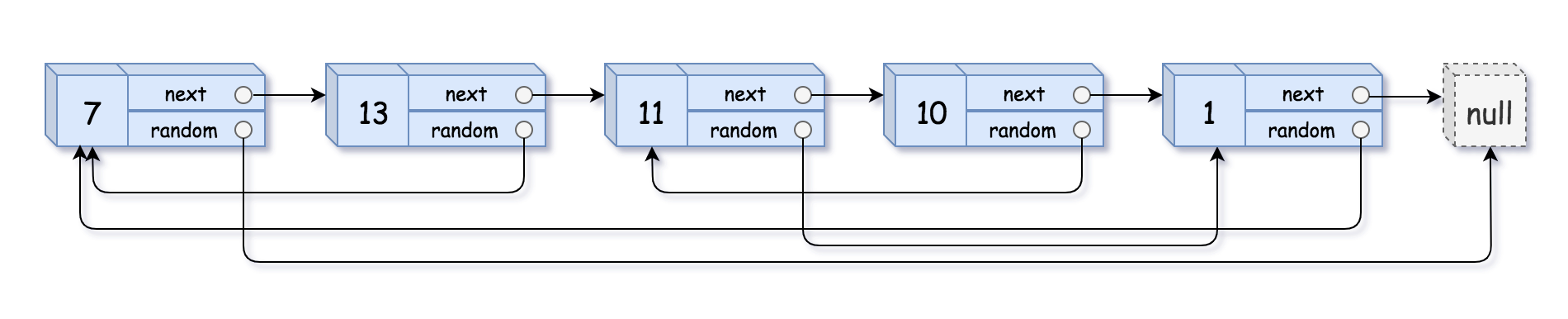
输入：head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
输出：[[7,null],[13,0],[11,4],[10,2],[1,0]]

示例 2：

输入：head = [[1,1],[2,1]]
输出：[[1,1],[2,1]]

解题思路

这道题如果采用最直接的方式，第一步先从头到位遍历一遍，先复制原始链表上的每一个结点，并用m_pNext链接起来；第二步，再次遍历，设置每个结点的random 指针。

假设原始链表中的某个结点 N 的 random 指向结点S，由于S的位置在链表中可能在N的前面也可能在N的后面，所以要定位 S 的位置需要从原始链表的头结点开始找。如果从原始链表的头结点开始沿着 next 经过 s 步找到结点S，那么在复制链表上结点 N’的 random（记为 S’）离复制链表的头结点的距离也是沿着 next 指针 s 步。

这种方式，由于定位每个结点的 random 都需要从链表头结点开始经过O（n）步才能找到，因此这种方法的总时间复杂度是O（n2）。

优化方案 1

在第一次遍历的时候，顺便构造一个 Hash，维护 N 到 N’ 的映射（即原节点与复制节点的映射），当设置 random 指针的时候，就可以通过映射快速找到对应的复制节点。

这种方式采用空间换时间的方式，以O（n）的空间消耗把时间复杂度由O（n2）降低到O（n）

优化方案 2（最优解）

最优解的方式可以在 O(1) 的空间下实现是 O（n）的时间。

第三种方法的第一步仍然是根据原始链表的每个结点 N创建对应的N’。但是把 N’链接在 N 的后面。下图的链表是经过这一步之后的结构：

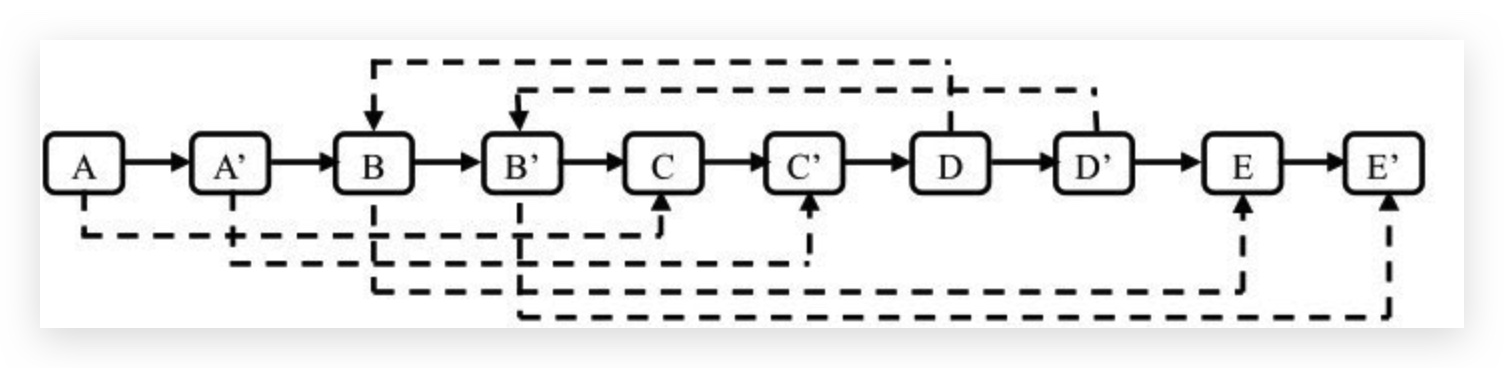
第二步设置复制出来的结点的 random。假设原始链表上的 N 的 random 指向结点S，那么其对应复制出来的 N’ 是N的 next 指向的结点，同样 S’ 也是 S 的 next 指向的结点。

第三步就是对链表进行拆解，把奇数位置的结点用 next 链接起来就是原始链表，把偶数位置的结点用 next 链接起来就是复制出来的链表。

代码实现

type Node struct {
    Val    int
    Next   *Node
    Random *Node
}

func copyRandomList(head *Node) *Node {
    if head == nil {
        return nil
    }
    head = appendNode(head)
    head = setRandomNode(head)
    head, copyList := separateList(head)
    return copyList
}

// appendNode 追加节点到原节点后面
func appendNode(head *Node) *Node {
    p := head
    for p != nil {
        node := &Node{
            Val:  p.Val,
            Next: p.Next,
        }
        p.Next = node
        p = node.Next
    }
    return head
}

// setRandomNode 赋值 Random 信息
func setRandomNode(head *Node) *Node {
    p := head
    for p != nil {
        if p.Random != nil {
            p.Next.Random = p.Random.Next
        }
        p = p.Next.Next
    }
    return head
}

// separateList 拆解链表
func separateList(head *Node) (*Node, *Node) {
    p := head
    copyList := head.Next
    cp := copyList
    for p != nil {
        p.Next = cp.Next
        p = p.Next
        // 有可能已经到了最后的节点
        if p != nil {
            cp.Next = p.Next
        } else {
            cp.Next = nil
        }
        cp = cp.Next
    }
    return p, copyList
}

包含 Min 函数的栈

剑指 Offer 第 30 题

定义栈的数据结构，请在该类型中实现一个能够得到栈的最小元素的 min 函数在该栈中，调用 min、push 及 pop 的时间复杂度都是 O(1)。

示例:

MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.min();   --> 返回 -3.
minStack.pop();
minStack.top();      --> 返回 0.
minStack.min();   --> 返回 -2.

解题思路

看到这个问题，我们的第一反应可能是每次压入一个新元素进栈时，将栈里的所有元素排序，让最小的元素位于栈顶，这样就能在O（1）时间得到最小元素了。

但这种思路不能保证最后压入栈的元素能够最先出栈，因此这个数据结构已经不是栈了。

我们接着想到在栈里添加一个成员变量存放最小的元素。每次压入一个新元素进栈的时候，如果该元素比当前最小的元素还要小，则更新最小元素。

这里会有问题：如果当前最小的元素被弹出栈了，如何得到下一个最小的元素呢？

分析到这里我们发现仅仅添加一个成员变量存放最小元素是不够的，也就是说当最小元素被弹出栈的时候，我们希望能够得到次小元素。因此在压入这个最小元素之前，我们要把次小元素保存起来。

是不是可以把每次的最小元素（之前的最小元素和新压入栈的元素两者的较小值）都保存起来放到另外一个辅助栈里呢？举个例子：

首先往空的数据栈里压入数字3，显然现在3是最小值，我们也把这个最小值压入辅助栈。接下来往数据栈里压入数字4。由于4大于之前的最小值，因此我们仍然往辅助栈里压入数字3。第三步继续往数据栈里压入数字2。由于2小于之前的最小值3，因此我们把最小值更新为2，并把2压入辅助栈。同样当压入数字1时，也要更新最小值，并把新的最小值1压入辅助栈。

步骤	操作	数据栈	辅助栈	最小值
1	压入 3	3	3	3
2	压入 4	3,4	3,3	3
3	压入 2	3,4,2	3,3,2	2
4	压入 1	3,4,2,1	3,3,2,1	1
5	弹出	3,4,2	3,3,2	2
6	弹出	3,4	3,3	3
7	压入 0	3,4,0	3,3,0	0

可以看到使用辅助栈就可以解决这个问题了。

代码实现

type MinStack struct {
    dataStack   []int // 存放真实数据的栈
    minNumStack []int // 存放当前最小值的栈
}

func Constructor() MinStack {
    return MinStack{}
}

func (this *MinStack) Push(x int) {
    this.dataStack = append(this.dataStack, x)
    if len(this.minNumStack) == 0 {
        this.minNumStack = append(this.minNumStack, x)
        return
    }
    curMinNum := this.minNumStack[len(this.minNumStack)-1]
    if curMinNum > x {
        this.minNumStack = append(this.minNumStack, x)
        return
    }
    this.minNumStack = append(this.minNumStack, curMinNum)
}

func (this *MinStack) Pop() {
    if len(this.dataStack) == 0 {
        return
    }
    this.dataStack = this.dataStack[:len(this.dataStack)-1]
    this.minNumStack = this.minNumStack[:len(this.minNumStack)-1]
}

func (this *MinStack) Top() int {
    if len(this.dataStack) == 0 {
        return 0
    }
    return this.dataStack[len(this.dataStack)-1]
}

func (this *MinStack) Min() int {
    if len(this.minNumStack) == 0 {
        return 0
    }
    return this.minNumStack[len(this.minNumStack)-1]
}

栈的压入、弹出序列

剑指 Offer 31 题

输入两个整数序列，第一个序列表示栈的压入顺序，请判断第二个序列是否为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如，序列 {1,2,3,4,5} 是某栈的压栈序列，序列 {4,5,3,2,1} 是该压栈序列对应的一个弹出序列，但 {4,3,5,1,2} 就不可能是该压栈序列的弹出序列。

示例 1：

输入：pushed = [1,2,3,4,5], popped = [4,5,3,2,1]
输出：true
解释：我们可以按以下顺序执行：
push(1), push(2), push(3), push(4), pop() -> 4,
push(5), pop() -> 5, pop() -> 3, pop() -> 2, pop() -> 1

实例 2：

输入：pushed = [1,2,3,4,5], popped = [4,3,5,1,2]
输出：false
解释：1 不能在 2 之前弹出。

实现思路

如下图所示，给定一个压入序列 pushed 和弹出序列 popped ，则压入 / 弹出操作的顺序（即排列）是 唯一确定 的。

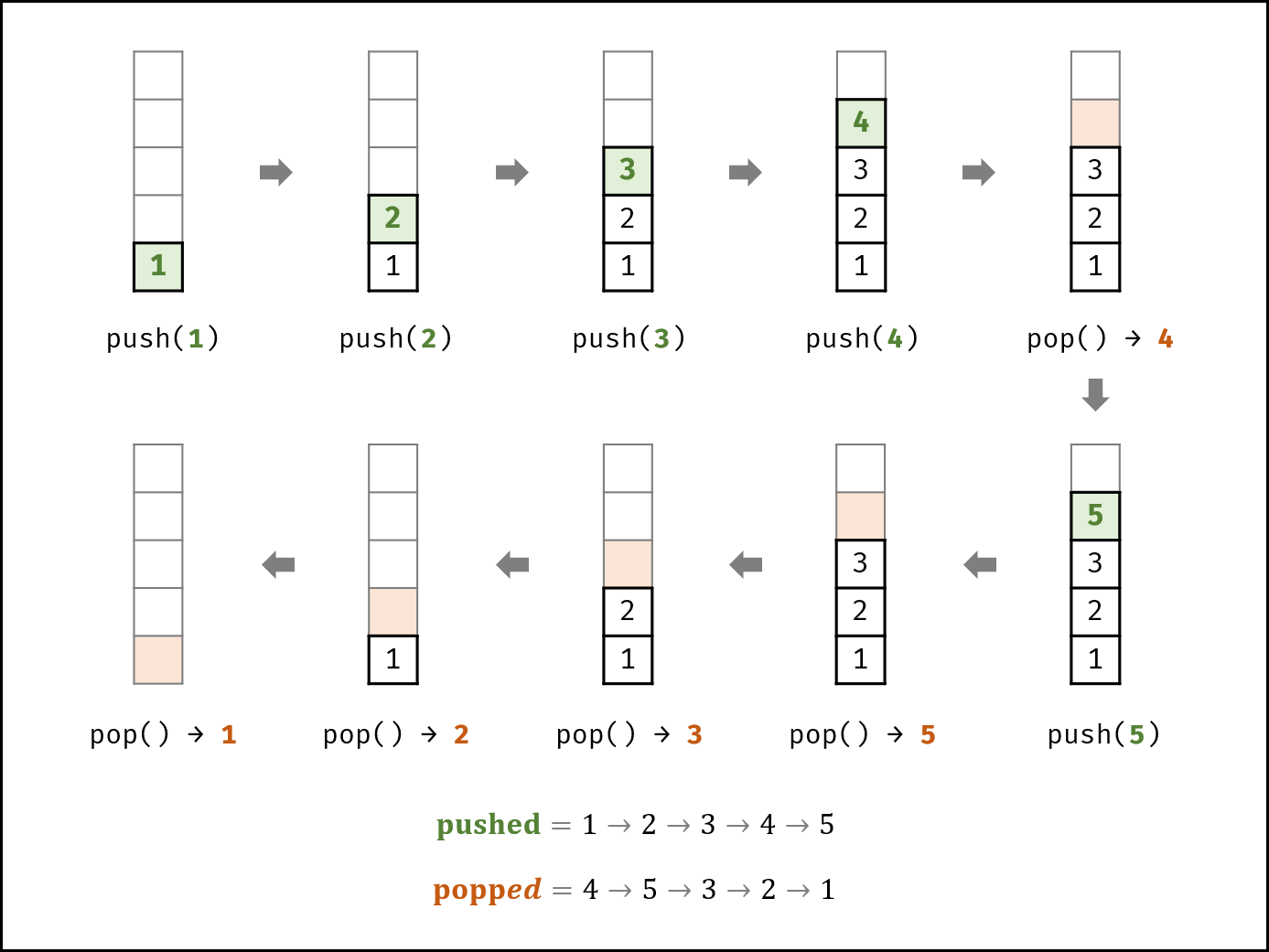
如下图所示，栈的数据操作具有 先入后出 的特性，因此某些弹出序列是无法实现的。

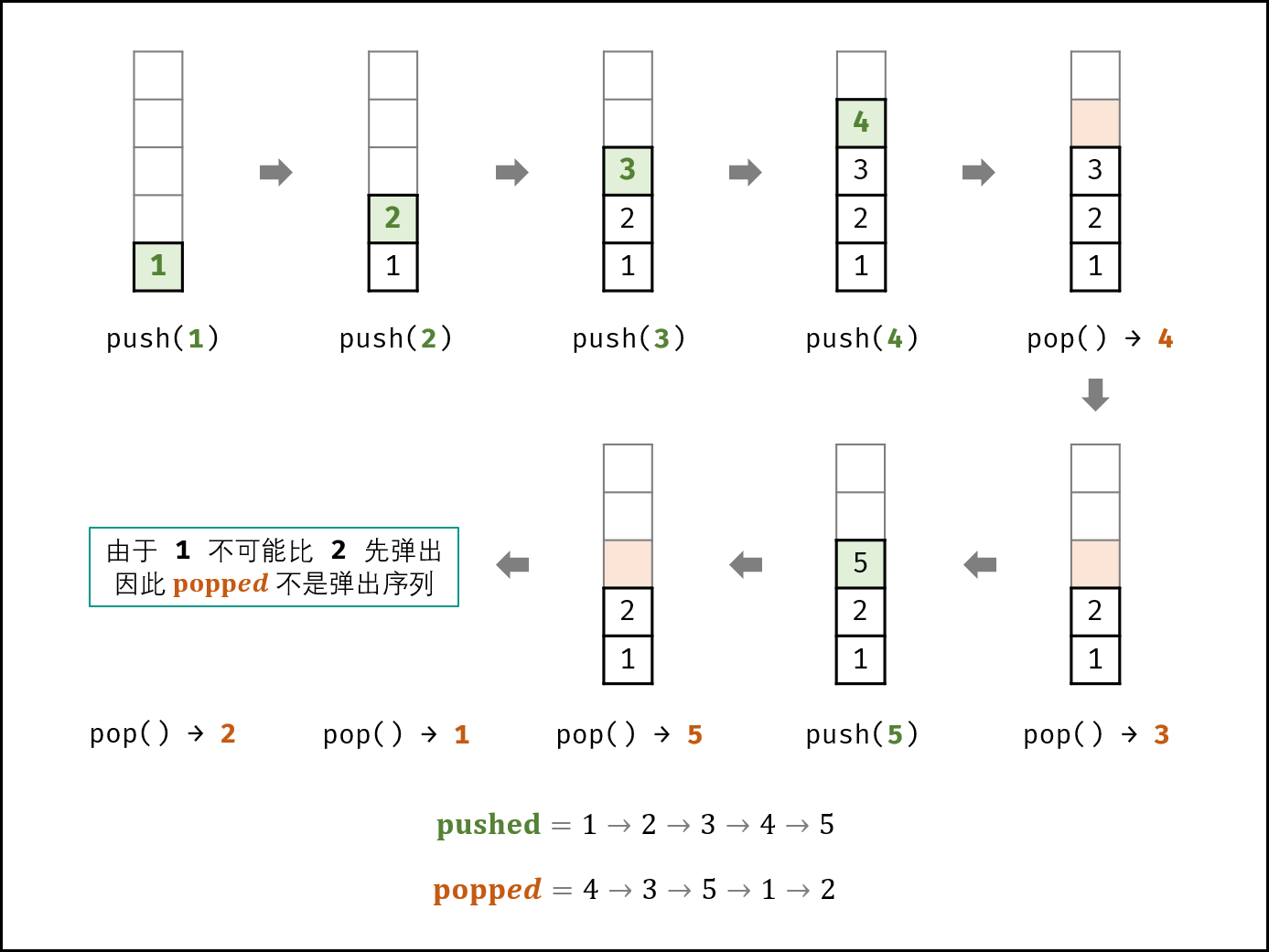
考虑借用一个辅助栈 stack ，模拟 压入 / 弹出操作的排列。根据是否模拟成功，即可得到结果。

• 入栈操作： 按照压栈序列的顺序执行。

• 出栈操作： 每次入栈后，循环判断 “栈顶元素 == 弹出序列的当前元素” 是否成立，将符合弹出序列顺序的栈顶元素全部弹出。

由于题目规定栈的所有数字均不相等 ，因此在循环入栈中，每个元素出栈的位置的可能性是唯一的（若有重复数字，则具有多个可出栈的位置）。因而，在遇到 “栈顶元素 == 弹出序列的当前元素” 就应立即执行出栈。

算法流程：

1. 初始化： 辅助栈 stack ，弹出序列的索引 i；
2. 遍历压栈序列： 各元素记为 num ；
   • 元素 num 入栈；
   • 循环出栈：若 stack 的栈顶元素 == 弹出序列元素 popped[i] ，则执行出栈与 i++ ；
3. 返回值： 若 stack 为空，则此弹出序列合法。

代码实现

func validateStackSequences(pushed []int, popped []int) bool {
    if len(pushed) != len(popped) {
        return false
    }

    // pushed = [1,2,3,4,5], popped = [4,5,3,2,1]
    var stack []int
    var pIndex int
    for i := range pushed {
        stack = append(stack, pushed[i])
        for len(stack) != 0 && stack[len(stack)-1] == popped[pIndex] {
            stack = stack[:len(stack)-1]
            pIndex++
        }
    }
    return len(stack) == 0
}

复杂度分析：

• 时间复杂度 O(N) ： 其中 N 为列表 pushed 的长度；每个元素最多入栈与出栈一次，即最多共 2N 次出入栈操作。
• 空间复杂度 O(N) ： 辅助栈 stack 最多同时存储 N 个元素。

两个栈实现队列

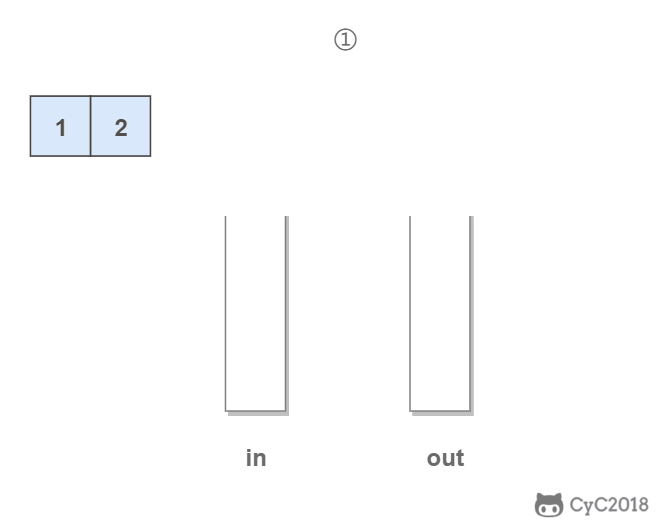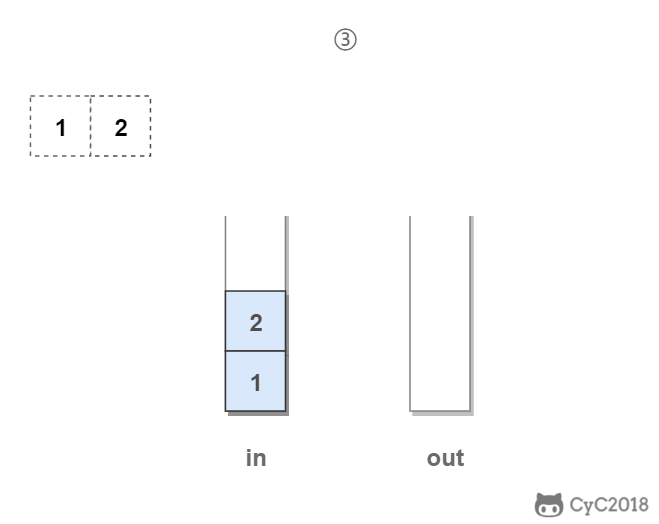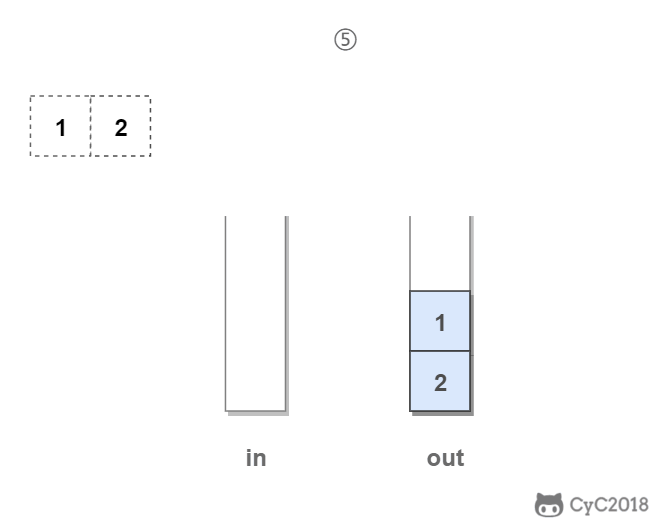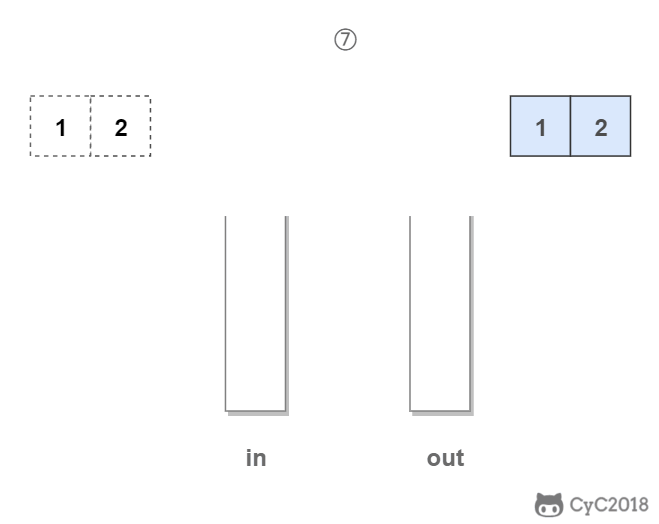
in 栈用来处理入栈（push）操作，out 栈用来处理出栈（pop）操作。一个元素进入 in 栈之后，出栈的顺序被反转。当元素要出栈时，需要先进入 out 栈，此时元素出栈顺序再一次被反转，因此出栈顺序就和最开始入栈顺序是相同的，先进入的元素先退出，这就是队列的顺序。

Stack<Integer> in = new Stack<Integer>();
Stack<Integer> out = new Stack<Integer>();

public void push(int node) {
    in.push(node);
}

public void pop() {
    if(out.isEmpty()) {
        while(!in.isEmpty()) {
            out.push(in.pop());
        }
    }
    
    if (out.isEmpty())
        throw new Exception("queue is empty");
    
    return out.pop();
}

go版本：

type CQueue struct {
    inStack  []int // 输入栈
    outStack []int // 输出栈
}

func Constructor() CQueue {
    return CQueue{}
}

func (this *CQueue) AppendTail(value int) {
    this.inStack = append(this.inStack, value)
}

func (this *CQueue) DeleteHead() int {
    outLen := len(this.outStack)
    if outLen != 0 {
        val := this.outStack[outLen-1]
        this.outStack = this.outStack[:outLen-1]
        return val
    }

    inLen := len(this.inStack)
    if inLen == 0 {
        return -1
    }
    var i = inLen - 1
    for ; i > 0; i-- {
        this.outStack = append(this.outStack, this.inStack[i])
    }
    val := this.inStack[i]
    this.inStack = []int{}
    return val
}

二叉搜索树转双向链表

Leecode:输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点，只能调整树中节点指针的指向。

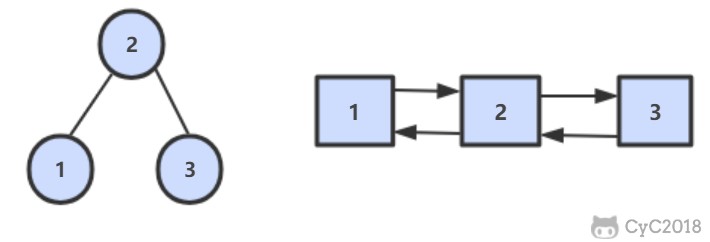
递归方式：改写中序遍历，遍历过程中使用一全局变量 pre 存储其前一个结点,当遍历该结点时，只需该节点的前驱(left)指向pre，pre的后继指向该节点。对于头结点应特殊处理。

private TreeNode pre = null;
private TreeNode head = null;

public TreeNode Convert(TreeNode root) {
    inOrder(root);
    return head;
}

private void inOrder(TreeNode node) {
    if (node == null)
        return;
    inOrder(node.left);
    node.left = pre;
    if (pre != null)
        pre.right = node;
    pre = node;
    if (head == null)
        head = node;
    inOrder(node.right);
}

非递归版本：

    public Node treeToDoublyList(Node root) {
        if(root == null){
            return null;
        }
         Stack<Node> stack = new Stack<>();
         Node current = root;
         Node pre = null, head = null, tail = null;
         while(!stack.isEmpty() || current != null) {
             while(current != null) {
                 stack.push(current);
                 current = current.left;
             }
             current = stack.pop();
             tail = current;
             if(pre == null) {//处理头结点
                 head = current;
             }else {
                 pre.right = current;
                 current.left = pre;
             }
            pre = current;
            current = current.right;
         }
         tail.right = head;
         head.left = tail;
         return head;
    }

Go 版本：

非递归实现：

type TreeNode struct {
    Val   int
    Left  *TreeNode
    Right *TreeNode
}

func Convert(pRootOfTree *TreeNode) *TreeNode {
    if pRootOfTree == nil {
        return nil
    }
    var st []*TreeNode
    var pre, head *TreeNode
    // 设想最左叶子结点和最右叶子节点的场景
    for len(st) != 0 || pRootOfTree != nil {
        for pRootOfTree != nil {
            st = append(st, pRootOfTree)
            pRootOfTree = pRootOfTree.Left
        }
        curr := st[len(st)-1]
        st = st[:len(st)-1]
        if pre != nil {
            pre.Right = curr
        } else {
            head = curr
        }
        curr.Left = pre
        pre = curr
        pRootOfTree = curr.Right
    }
    return head
}

递归版本：

func Convert2(root *TreeNode) *TreeNode {
    var dfs func(cur *TreeNode)
    var pre, head *TreeNode
    dfs = func(cur *TreeNode) {
        if cur == nil {
            return
        }
        dfs(cur.Left)
        if pre != nil {
            pre.Right = cur
        } else {
            head = cur
        }
        cur.Left = pre
        pre = cur
        dfs(cur.Right)
    }
    dfs(root)
    return head
}

有序链表转换二叉搜索树

Leecode:给定一个单链表，其中的元素按升序排序，将其转换为高度平衡的二叉搜索树。

本题中，一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。

示例:

给定的有序链表： [-10, -3, 0, 5, 9],

一个可能的答案是：[0, -3, 9, -10, null, 5], 它可以表示下面这个高度平衡二叉搜索树：

      0
     / \
   -3   9
   /   /
 -10  5

解题思路：给定列表中的中间元素将会作为二叉搜索树的根，该点左侧的所有元素递归的去构造左子树，同理右侧的元素构造右子树。这必然能够保证最后构造出的二叉搜索树是平衡的。

1. 由于我们得到的是一个有序链表而不是数组，我们不能直接使用下标来访问元素。我们需要知道链表中的中间元素。
2. 我们可以利用两个指针来访问链表中的中间元素。假设我们有两个指针 slow_ptr 和 fast_ptr。slow_ptr 每次向后移动一个节点而 fast_ptr 每次移动两个节点。当 fast_ptr 到链表的末尾时 slow_ptr 就访问到链表的中间元素。对于一个偶数长度的数组，中间两个元素都可用来作二叉搜索树的根。
3. 当找到链表中的中间元素后，我们将链表从中间元素的左侧断开，做法是使用一个 prev_ptr 的指针记录 slow_ptr 之前的元素，也就是满足 prev_ptr.next = slow_ptr。断开左侧部分就是让 prev_ptr.next = None。
4. 我们只需要将链表的头指针传递给转换函数，进行高度平衡二叉搜索树的转换。所以递归调用的时候，左半部分我们传递原始的头指针；右半部分传递 slow_ptr.next 作为头指针。

class Solution {

  private ListNode findMiddleElement(ListNode head) {

    // The pointer used to disconnect the left half from the mid node.
    ListNode prevPtr = null;
    ListNode slowPtr = head;
    ListNode fastPtr = head;

    // Iterate until fastPr doesn't reach the end of the linked list.
    while (fastPtr != null && fastPtr.next != null) {
      prevPtr = slowPtr;
      slowPtr = slowPtr.next;
      fastPtr = fastPtr.next.next;
    }

    // Handling the case when slowPtr was equal to head.
    if (prevPtr != null) {
      prevPtr.next = null;
    }

    return slowPtr;
  }

  public TreeNode sortedListToBST(ListNode head) {

    // If the head doesn't exist, then the linked list is empty
    if (head == null) {
      return null;
    }

    // Find the middle element for the list.
    ListNode mid = this.findMiddleElement(head);

    // The mid becomes the root of the BST.
    TreeNode node = new TreeNode(mid.val);

    // Base case when there is just one element in the linked list
    if (head == mid) {
      return node;
    }

    // Recursively form balanced BSTs using the left and right halves of the original list.
    node.left = this.sortedListToBST(head);
    node.right = this.sortedListToBST(mid.next);
    return node;
  }
}

从前序与中序遍历序列构造二叉树

剑指offer第7题

根据一棵树的前序遍历与中序遍历构造二叉树。

注意: 可以假设树中没有重复的元素。

例如，给出：

前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]

返回如下的二叉树：

        3
   / \
  9  20
    /  \
   15   7

解题思路：

根据前序遍历结果，首节点一定是根结点，在中序遍历中找到根结点，根节点左边的都是左子树，根结点右边的都是右子树。

另外，由于是遍历同一颗树，所以左子树和右子树的节点数量是相同的。利用这个关系，可以定义出如下边界：

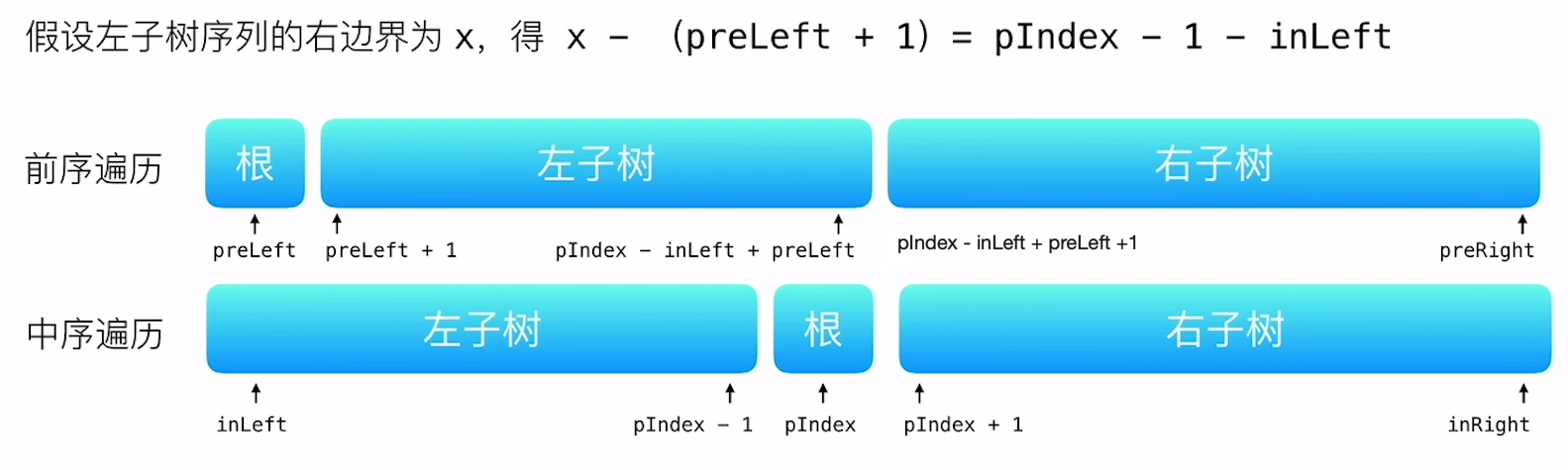
接下来就只需要分别递归构建左右子树即可：

public class RebuildBinaryTree {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        int preLen = preorder.length;
        int inLen = inorder.length;
        HashMap<Integer, Integer> map = new HashMap<Integer, Integer>(inLen);
        // 构造中序遍历中根结点和下标的映射关系
        for (int i = 0; i < inLen; i++) {
            map.put(inorder[i], i);
        }
        return buildTree(preorder, 0, preLen - 1, 0, inLen - 1, map);
    }

    /**
     * 递归构建二叉树
     * @param preorder 前序遍历结果
     * @param preLeft 当前前序遍历根结点（当前遍历的最左边界）
     * @param preRight 当前前序遍历的最又边界
     * @param inLeft 当前中序遍历的最左边界
     * @param inRight 当前中序遍历的最右边界
     * @param map 存储根结点在中序遍历的映射关系
     * @return 二叉树
     */
    private TreeNode buildTree(int[] preorder, int preLeft, int preRight,
                               int inLeft, int inRight, HashMap<Integer, Integer> map) {
        if (preLeft > preRight || inLeft > inRight) {
            return null;
        }
        TreeNode head = new TreeNode(preorder[preLeft]);
        Integer pIndex = map.get(preorder[preLeft]);
        head.left = buildTree(preorder, preLeft + 1, pIndex - inLeft + preLeft,
                inLeft, pIndex - 1, map);
        head.right = buildTree(preorder, pIndex - inLeft + preLeft + 1,
                preRight, pIndex + 1, inRight, map);
        return head;
    }
}

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    public TreeNode(int val) {
        this.val = val;
    }
}

go 版本：

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func buildTree(preorder []int, inorder []int) *TreeNode {
if len(preorder) == 0 {
        return nil
    }

    // 先构建一个 inroder 数值到下标的映射
    inVal2Idx := make(map[int]int, len(inorder))
    for i, val := range inorder {
        inVal2Idx[val] = i
    }

    head := constructTreeNode(preorder, inVal2Idx, 0, len(preorder)-1, 0, len(inorder)-1)
    return head
}

func constructTreeNode(preorder []int, inVal2Idx map[int]int,
    preLeft, preRight, inLeft, inRight int) *TreeNode {
    if preLeft > preRight || inLeft > inRight {
        return nil
    }

    rootVal := preorder[preLeft]
    node := &TreeNode{Val: rootVal}
    inValIdx := inVal2Idx[rootVal]
    node.Left = constructTreeNode(preorder, inVal2Idx,
        preLeft+1, inValIdx-inLeft+preLeft, inLeft, inValIdx-1)
    node.Right = constructTreeNode(preorder, inVal2Idx,
        inValIdx-inLeft+preLeft+1, preRight, inValIdx+1, inRight)
    return node
}

复杂度分析

• 时间复杂度：O(n)，其中 n 是树中的节点个数。
• 空间复杂度：O(n)，除去返回的答案需要的 O(n) 空间之外，我们还需要使用 O(h)（其中 h 是树的高度）的空间存储栈。这里 h < n，所以（在最坏情况下）总空间复杂度为 O(n)。

从上往下打印二叉树

剑指 offer 32 题

从上往下打印出二叉树的每个结点，同一层的结点按照从左到右的顺序打印。例如:

给定二叉树: [3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7

返回：

[3,9,20,15,7]

解题思路

这道题实质是考查树的遍历算法，只是这种遍历不是熟悉的前序、中序或者后序遍历。

不妨先分析一下上述二叉树打印的过程。因为按层打印的顺序决定应该先打印根结点，所以从树的根结点开始分析。为了接下来能够打印值为 3 的结点的两个子结点，应该在遍历到该结点时把值为 9 和 20 的两个结点保存到一个容器里，现在容器内就有两个结点了。

按照从左到右打印的要求，先取出值为 9 的结点。打印出值 9 之后，取出 20 ，再把它的值分别为 15 和 7 的两个结点放入数据容器。此时数据容器中有2个结点，值分别为 15 和 7。

这里可以看出采用先入先出的规则来进行，即利用了辅助队列。

代码实现

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func levelOrder(root *TreeNode) []int {
    if root == nil {
        return nil
    }
    var ret []int
    var cacheQueue []*TreeNode
    cacheQueue = append(cacheQueue,root)

    for len(cacheQueue) != 0 {
        node := cacheQueue[0]
        cacheQueue = cacheQueue[1:]
        ret = append(ret,node.Val)
        if node.Left != nil {
            cacheQueue = append(cacheQueue,node.Left)
        }
        if node.Right != nil {
            cacheQueue = append(cacheQueue,node.Right)
        }
    }
    return ret
}

二叉搜索树的后序遍历序列

剑指 offer 33 题

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true，否则返回 false。假设输入的数组的任意两个数字都互不相同。

参考以下这颗二叉搜索树：

     5
    / \
   2   6
  / \
 1   3

示例 1：

输入: [1,6,3,2,5]
输出: false

示例 2：

输入: [1,3,2,6,5]
输出: true

在后序遍历得到的序列中，最后一个数字是树的根结点的值。数组中前面的数字可以分为两部分：第一部分是左子树结点的值，它们都比根结点的值小；第二部分是右子树结点的值，它们都比根结点的值大。

以数组{1,3,2,6,5}为例，后序遍历结果的最后一个数字5就是根结点的值。在这个数组中，前3个数字1,3,2都比5小，是值为5的结点的左子树结点；后1个数字6比5大，是值为5的结点的右子树结点。接下来用同样的方法确定与数组每一部分对应的子树的结构。这其实就是一个递归的过程。对于序列1,3,2，最后一个数字2是左子树的根结点的值。数字1比2小，是值为2的结点的左子结点，而3则是它的右子结点。

通过这个规律就可以实现代码逻辑了。

代码实现

func verifyPostorder(postorder []int) bool {
    if len(postorder) == 0 {
        return true
    }
    // 根节点数值
    tail := postorder[len(postorder)-1]

    postorder = postorder[:len(postorder)-1]
    var left, right []int
    var div bool // 区分是否已经到了左右子树分割点
    for i := range postorder {
        // 小于最后的节点，并且前面已经出现大于最后节点的数了
        if postorder[i] < tail && div {
            return false
        }
        if postorder[i] < tail {
            left = append(left, postorder[i])
            i++
            continue
        }
        right = append(right, postorder[i])
        i++
        div = true
    }
    return verifyPostorder(left) && verifyPostorder(right)
}

二叉树中和为某一值的路径

Leecode:输入一棵二叉树和一个整数，打印出二叉树中节点值的和为输入整数的所有路径。从树的根节点开始往下一直到叶节点所经过的节点形成一条路径。

解题思路

由于路径是从根结点出发到叶结点，也就是说路径总是以根结点为起始点，因此首先需要遍历根结点。在树的前序、中序、后序三种遍历方式中，只有前序遍历是首先访问根结点的。

当用前序遍历的方式访问到某一结点时，我们把该结点添加到路径上，并累加该结点的值。如果该结点为叶结点，并且路径中结点值的和刚好等于输入的整数，则当前的路径符合要求，这时候把它打印出来。

如果当前结点不是叶结点，则继续访问它的子结点。当前结点访问结束后，递归函数将自动回到它的父结点。因此在函数退出之前要在路径上删除当前结点并减去当前结点的值，以确保返回父结点时路径刚好是从根结点到父结点的路径。

不难看出保存路径的数据结构实际上是一个栈，因为路径要与递归调用状态一致，而递归调用的本质就是一个压栈和出栈的过程。

代码实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    //存储结果集
    List<List<Integer>> result = new ArrayList<>();
    //存储每一条路径
    List<Integer> path = new ArrayList<>();

    public List<List<Integer>> pathSum(TreeNode root, int sum) {
        recur(root,sum);
        return result;
    }

    private void recur(TreeNode root,int sum) {
        if(root == null) {
            return;
        }
        sum -= root.val;
        path.add(root.val);
        //当左右子树都为空说明已经到了叶子结点，如果 sum 已经减为 0，说明该路径可以，加入结果集
        if(root.left == null && root.right == null && sum == 0) {
            //需要拷贝路径加入，直接加入的话后续path一变会导致结果集的数据跟着改变
            result.add(new ArrayList<>(path));
        }
        //递归左子节点
        recur(root.left,sum);
        //递归右子节点
        recur(root.right,sum);
        //路径恢复，向上回溯前，需要将当前节点从路径 path 中删除
        path.remove(path.size()-1);
    }
}

go 版本：

func pathSum(root *TreeNode, target int) [][]int {
    if root == nil {
        return nil
    }
    var ret [][]int
    getPath(target, root, []int{}, &ret)
    return ret
}

func getPath(target int, node *TreeNode, path []int, ret *[][]int) {
    if node == nil {
        return
    }
    gap := target - node.Val
    // 不能判断小于0，因为有可能节点里的是负数
    //if gap < 0 {
    //	return
    //}
    path = append(path, node.Val)
    if gap == 0 && node.Left == nil && node.Right == nil {
        // 这里要把 path copy 出来，防止后面被更改，这里是 copy 了一个指针，内部标明了切片 start和 end 坐标
        *ret = append(*ret, append([]int(nil), path...))
        path = path[:len(path)-1]
        return
    }
    getPath(gap, node.Left, path, ret)
    getPath(gap, node.Right, path, ret)
    path = path[:len(path)-1]
    return
}

• 时间复杂度 O(N)：N 为二叉树的节点数，先序遍历需要遍历所有节点。
• 空间复杂度 O(N)：最差情况下，即树退化为链表时，path 存储所有树节点，使用 O(N) 额外空间。

二叉树的最近公共祖先

Leecode:给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”
例如，给定如下二叉树:  root = [3,5,1,6,2,0,8,null,null,7,4]

解题思路：

递归，这种方法非常直观。先深度遍历改树。当遇到节点 p 或 q 时，返回一些布尔标记。该标志有助于确定是否在任何路径中找到了所需的节点。最近的祖先将是两个子树递归都返回真标志的节点。它也可以是一个节点，它本身是p或q中的一个，对于这个节点,子树递归返回一个真标志。

让我们看看基于这个想法的形式算法。

算法：

1. 从根节点开始遍历树。
2. 如果当前节点本身是 p 或 q 中的一个，我们会将变量 mid 标记为 true，并继续搜索左右分支中的另一个节点。
3. 如果左分支或右分支中的任何一个返回 true，则表示在下面找到了两个节点中的一个。
4. 如果在遍历的任何点上，左、右或中三个标志中的任意两个变为 true，这意味着我们找到了节点 p 和 q 的最近公共祖先。

class Solution {

    private TreeNode ans;

    public Solution() {
        this.ans = null;
    }

    private boolean recurseTree(TreeNode currentNode, TreeNode p, TreeNode q) {

        if (currentNode == null) {
            return false;
        }

        int left = this.recurseTree(currentNode.left, p, q) ? 1 : 0;
        int right = this.recurseTree(currentNode.right, p, q) ? 1 : 0;
        int mid = (currentNode == p || currentNode == q) ? 1 : 0;


        if (mid + left + right >= 2) {
            this.ans = currentNode;
        }

        return (mid + left + right > 0);
    }

    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        this.recurseTree(root, p, q);
        return this.ans;
    }
}

复杂度分析:

• 时间复杂度：O(N)，N 是二叉树中的节点数，最坏情况下，我们需要访问二叉树的所有节点。
• 空间复杂度：O(N)，这是因为递归堆栈使用的最大空间位 N,斜二叉树的高度可以是 N。

树的子结构

输入两棵二叉树A和B，判断B是不是A的子结构。(约定空树不是任意一个树的子结构)

B是A的子结构， 即 A中有出现和B相同的结构和节点值。

例如:

给定的树 A:

   3
  / \
 4   5
/ \
1  2

给定的树 B：

  4 
  /
 1

返回 true，因为 B 与 A 的一个子树拥有相同的结构和节点值。

示例 1：

输入：A = [1,2,3], B = [3,1]

输出：false

示例 2：

输入：A = [3,4,5,1,2], B = [4,1]

输出：true

解题思路

这里采用递归来实现会相对比较好理解一些。要查找树 A 中是否存在和树B结构一样的子树，可以分成两步：

第一步在树A中找到和B的根结点的值一样的结点R，第二步再判断树A中以R为根结点的子树是不是包含和树B一样的结构。

代码实现

func isSubStructure(A *TreeNode, B *TreeNode) bool {
    // 根据题目要求，只要有一个是 nil，那就是 false
    if A == nil || B == nil {
        return false
    }

    // 通过构造一个新函数，来解决 A 或者 B 为 nil 的冲突
    if isSame(A, B) {
        return true
    }

    // 相同根节点的子树不一样，用 A 的左子树和右子树继续递归查询
    return isSubStructure(A.Left, B) || isSubStructure(A.Right, B)
}

func isSame(A *TreeNode, B *TreeNode) bool {
    if A == nil && B != nil {
        return false
    }
    if B == nil {
        return true
    }
    if A.Val == B.Val {
        return isSame(A.Left, B.Left) && isSame(A.Right, B.Right)
    }
    return false
}

树的镜像

剑指 Offer 第 27 题

请完成一个函数，输入一个二叉树，该函数输出它的镜像。

例如输入：

             4
    /   \
  2     7
 / \   / \
1   3 6   9

镜像输出：

             4
    /   \
  7     2
 / \   / \
9   6 3   1

示例 1：

输入：root = [4,2,7,1,3,6,9]

输出：[4,7,2,9,6,3,1]

解题思路

这道题实际上就是在对树进行中序遍历，每次遍历到节点的时候，顺便交换一下左右子树即可。

代码实现

func mirrorTree(root *TreeNode) *TreeNode {
    if root == nil {
        return nil
    }

    root.Left, root.Right = root.Right, root.Left
    mirrorTree(root.Left)
    mirrorTree(root.Right)
    return root
}

一颗完全二叉树共有1699个结点，则该二叉树中叶子结点数（度为0）为？

在二叉树中有关系：度为0的结点个数 = 度为2的结点个数 + 1，表示为：n0 = n2 +1；
因为度为1的结点只可能出现在最后一个结点，或者根本就不存在度为1的结点。
假设:存在度为1的结点；
n0 + n2 + 1 = 1699，解其可得，n0 与 n2 都不为整数，这与事实不符，所以可以得出，不存在度数为1的点(虽然计算得出是的确不存在，但并不是一定不存在)
所以可得度为1的结点是不存在的；
即：n0 + n2 = 1699，解 n0 = 850

字典树（trie）实现敏感词汇过滤

trie 树也称为字典树、单词查找树，最大的特点就是共享字符串的公共前缀来达到节省空间的目的。

算法思路总结：

首先对需要屏蔽的词汇构建字典树（Trie Tree），然后创建三个指针，begin 指针指向匹配字符串起始位置，position 指针指向当前需要对比的字符，tempNode首先指向字典树的根节点。

每次 position 位置字符与 tempNode 子节点对比，如果不匹配则 position 和 begin 均加 1再继续比较；

如果匹配 tempNode 指向所匹配节点继续比较，同时 position+1，直到 tempNode 指向叶子节点则说明匹配到敏感词汇，将 begin 位置到 position 位置的字符屏蔽用 *代替,然后 position +1，begin 指向 position 位置，tempNode 指向跟节点，继续往下执行。

若匹配过程中到某一个 tempNode 节点时，其子节点已经没有匹配的字符，说明当前词汇不符合敏感词汇，则将 begin+1，同时 position 指向 begin，tempNode 再次指向根节点。

具体过程

首先建立个敏感词前缀树，根节点为空：

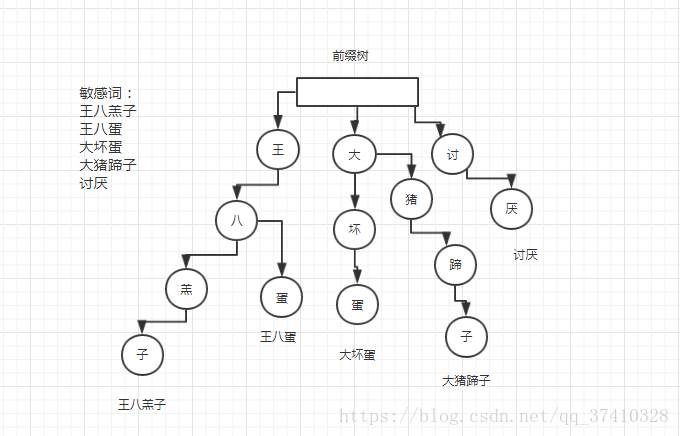
准备好待处理字符串：“哈哈大王八子大猪蹄子哦” ，声明三个指针，分别指向前缀树的根节点以及待处理字符串的开始字符

position 指向的字符与根节点的所有子节点进行匹配，不匹配，position 和 begin 分别指向待处理字符串的下一个字符，tempNode 依旧指向根节点

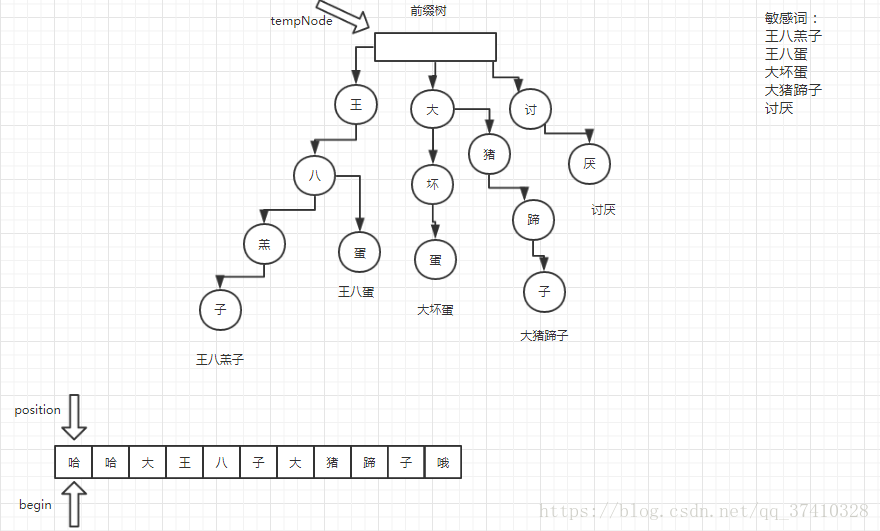
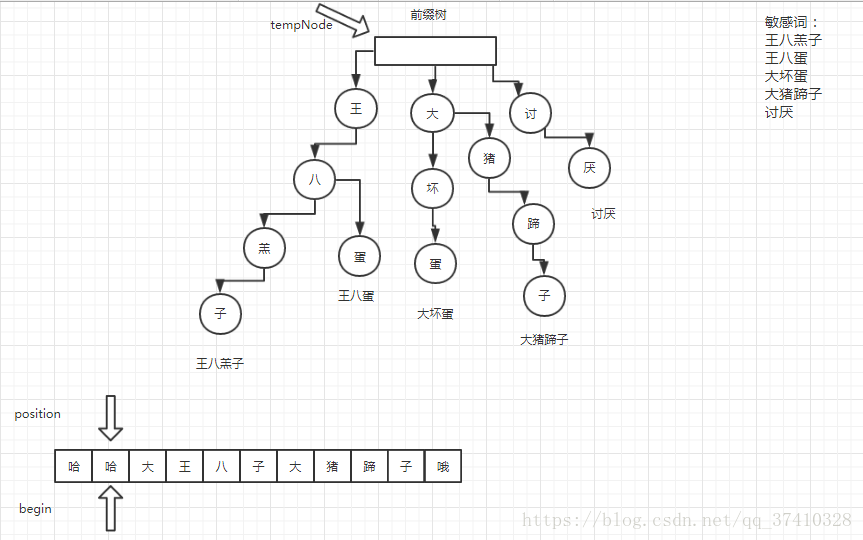
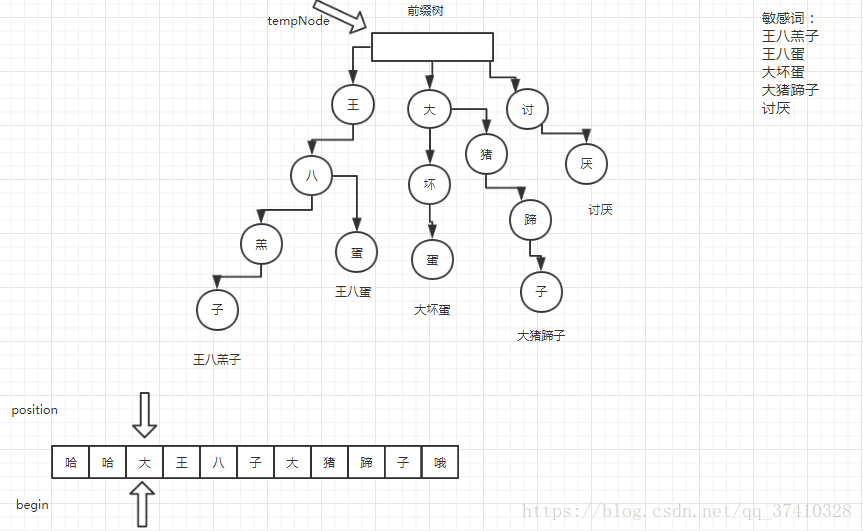
此时根节点有一个子节点与 position 指向的字符相等，都为‘大’，则 tempNode 指向该节点，同时 position 前进一步，指向‘王’

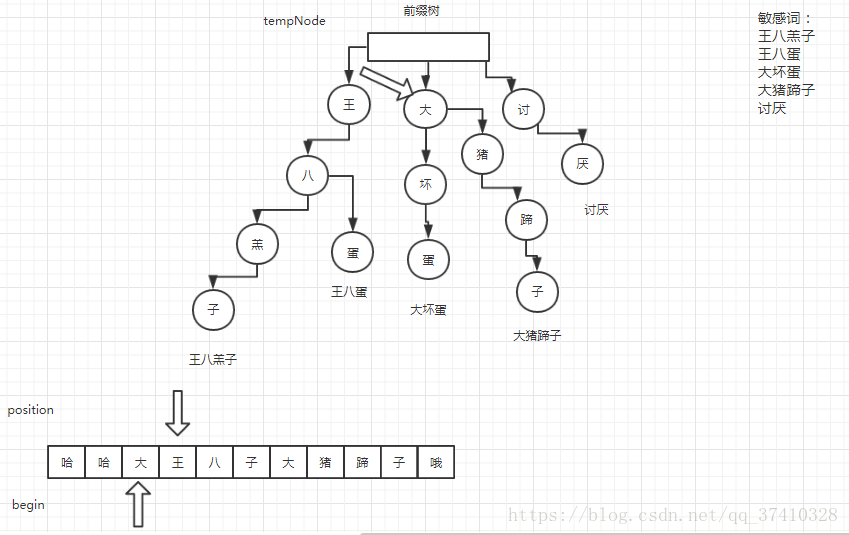
此时把 position 指向的‘王’ 和 tempNode 的所有子节点进行匹配，匹配失败，说明 从 begin 起头所有串是不存在敏感词的，可以直接输出。此时 begin 前进一位，position 回退到 begin 的位置，tempNode 回退到根节点

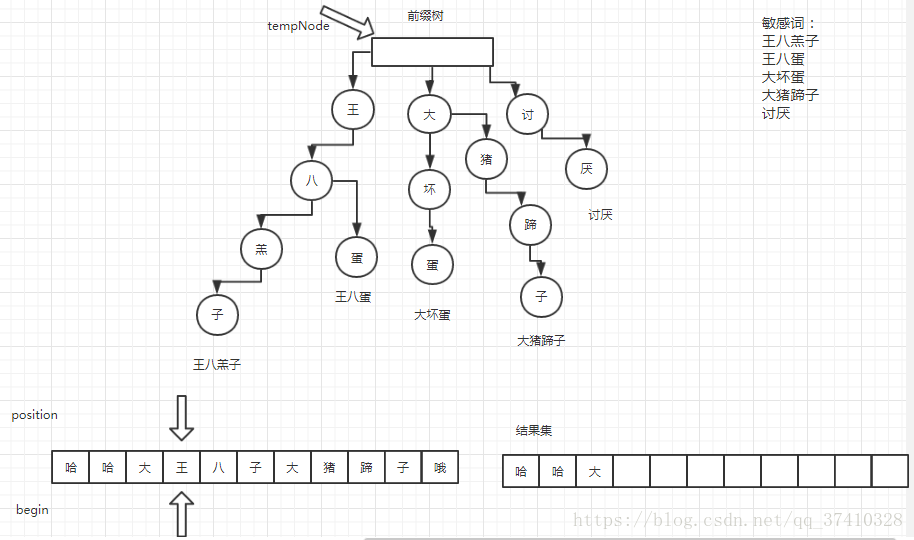
此时再把 position 指向的‘王’与 tempNode 的所有子节点进行匹配，匹配成功，所以 tempNode 指向该节点，同时 position 前进一位，指向’八’

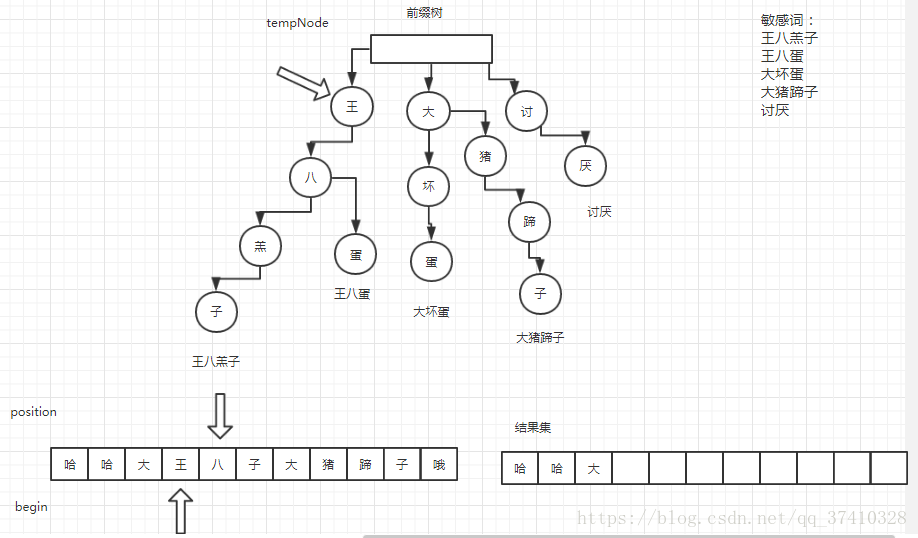
此时再把 position 指向的‘王’ 与 tempNode 的所有子节点进行匹配，匹配成功，此时 tempNode 指向它的子节点‘八’，同时 position 前进一位。

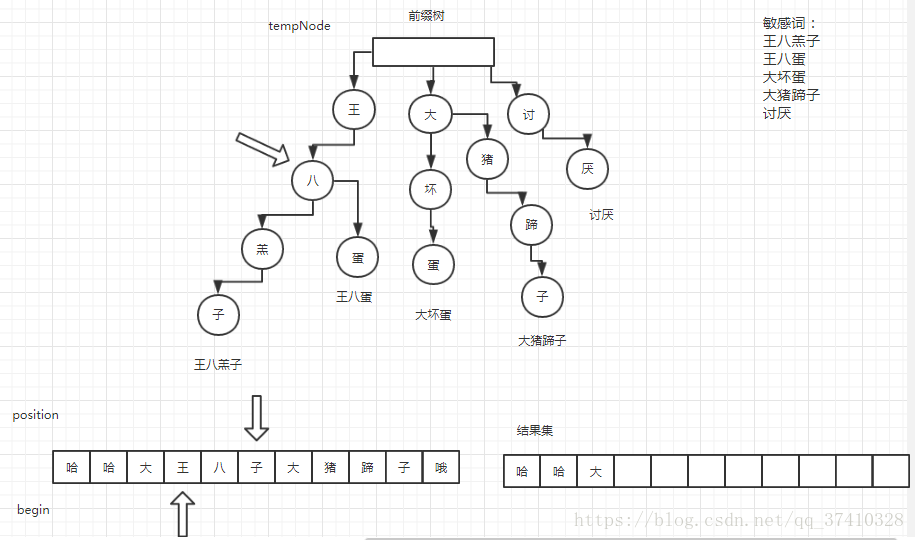
继续把 position 指向的字符 与tempNode 的所有子节点进行匹配，匹配失败。说明以begin起头的不存在非法字符，可以加入到结果集中。 此时 begin 向前走一位，position 回退到 begin 的位置，同时 tempNode 回退到根节点。

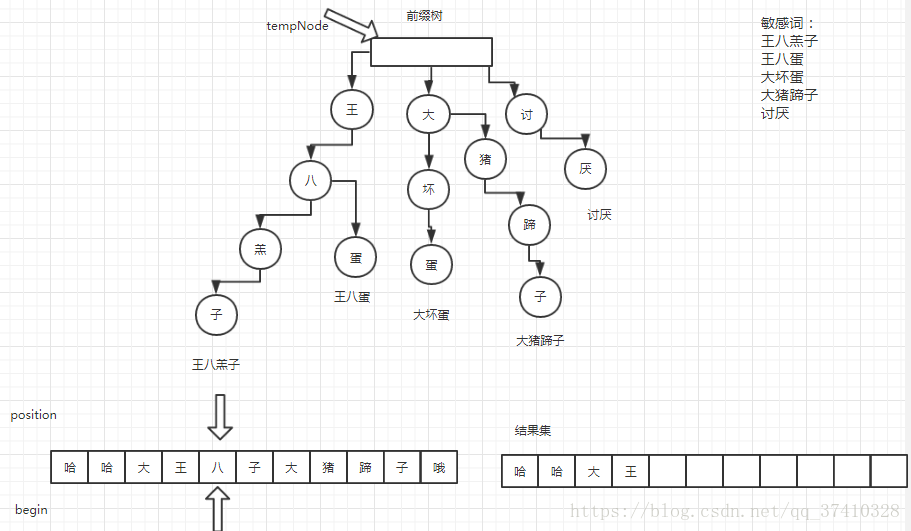
同理，可以发现子’子’不匹配，则直接把它加入结果集，同时position 和 begin 向前走一位，tempNode 指向根节点。

此时 position 指向 ‘大’，与 tempNode 的所有子节点进行匹配，匹配成功，则 position 和 tempNode 都走一位，循环执行….

直到 position 指向‘子’，tempNode指向‘蹄’（图中begin指针应该指向‘大’）

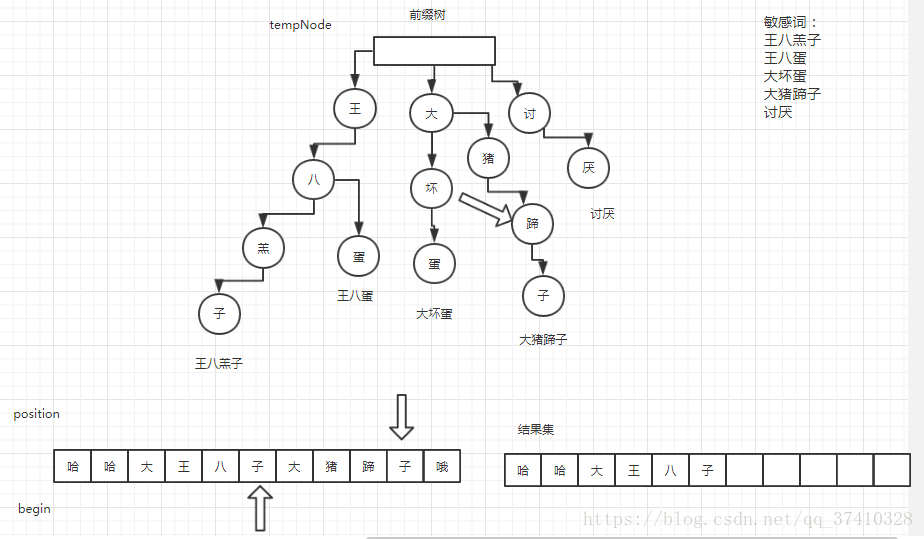
此时把 position 与 tempNode 的所有子节点进行匹配，匹配成功，tempNode 指向它的子节点‘子’，此时检查发现tempNode是敏感词树的叶子节点，说明从 begin 开始的位置到 position 这段是敏感词，用和谐词替换掉。替换之后 position 前进一位，begin 跳到 position 的位置，tempNode 回退到根节点

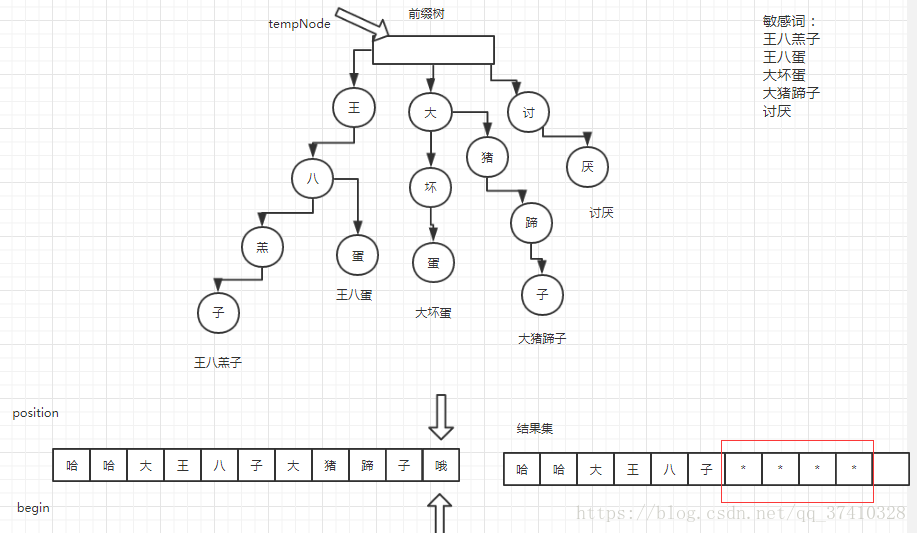
算法代码实现

前缀树结构：

private class TreeNode{
 
    //是否最后一个字
    private boolean isKeyWordsEnd = false;
 
    //子节点
    private Map<Character,TreeNode> subNodes = new HashMap<>();
 
    public void addSubNode(Character key, TreeNode node){
        subNodes.put(key,node);
    }
 
    public TreeNode getSubNode(Character key){
        return subNodes.get(key);
    }
 
    public boolean isKeyWordsEnd(){
        return isKeyWordsEnd;
    }
 
    public void setKeyWordsEnd(Boolean end){
        isKeyWordsEnd = end;
    }
}

构建前缀树的方法:

public void addSensitiveWord(String words){
 
    TreeNode tempNode = rootNode;
 
    for(int i = 0;  i < words.length(); i++){
 
        Character c = words.charAt(i);
        if(!isSymbol(c)){
            continue;
        }
 
        TreeNode node = tempNode.getSubNode(c);
        if (node == null){
            node = new TreeNode();
            tempNode.addSubNode(c,node);
        }
        // 指针移动
        tempNode = node;
 
        //如果到了最后一个字符
        if(i == words.length() -1){
            tempNode.setKeyWordsEnd(true);
        }
    }
}

算法具体实现：

public String filter(String text){
 
    if (StringUtils.isEmpty(text)){
        return text;
    }
 
    String sensitiveWords = "***";
    StringBuilder result = new StringBuilder();
 
    TreeNode tempNode = rootNode;
    int begin = 0;
    int position = 0;
 
    while (position < text.length()){

        Character c = text.charAt(position);
 
        //如果非匹配字符，则直接跳过
        if(!isSymbol(c)){ //每次
            if(tempNode == rootNode){
                result.append(c);
                begin++;
            }
            position++;
            continue;
        }
 
        tempNode = tempNode.getSubNode(c);
 
        //如果匹配失败
        if(tempNode == null) {
            //说明以begin起头的那一段不存在非法词汇
            result.append(text.charAt(begin));
            begin++;
            position = begin;
            tempNode = rootNode;
            continue;

        } else if(tempNode.isKeyWordsEnd()){
            //替换敏感词
            result.append(sensitiveWords);
            position++;
            begin = position;
            tempNode = rootNode;
        } else if(position > text.length() && (begin+1) < text.length()) {
                /** 
                 * 防止出现有相同后缀的敏感词汇
                 * 如fabcd，abc，当字符串最后fabc, 此时指begin指f, 
                 * 指position指到c, 根据循环中的判断c的isKeywordsEnd为true, 
                 * position++, 此时跳出循环, 然后将fabc加到StringBuilder中, 
                 * 但是abc这个敏感词没有被过滤掉
                 */
                begin = begin +1;
                position = begin;
                tempNode = rootNode;
                continue;
        } else {
            position++;
        }       
    }   
    result.append(text.substring(begin)); //把剩下的动加入合法集
 
    return result.toString();
}

时间空间复杂度

如果敏感词的长度为 m，则每个敏感词的查找时间复杂度是 O(m)，字符串的长度为 n，我们需要遍历 n 遍，所以敏感词查找这个过程的时间复杂度是 O(n * m)。如果有 t 个敏感词的话，构建 trie 树的时间复杂度是 O(t * m)。

给定已有硬币面值，计算需要的最少硬币数目？

使用动态规划的思想解决：

详情看这里

动态规划01背包问题

假设山洞里共有a,b,c,d ,e这5件宝物（不是5种宝物），它们的重量分别是2,2,6,5,4，它们的价值分别是6,3,5,4,6，现在给你个承重为10的背包, 怎么装背包，可以才能带走最多的财富。

状态：maxValue[i][j]表示前 i 个宝石装到剩余体积为 j 的背包里能达到的最大价值。

状态转移方程：maxValue[i][j] = max{maxValue[i-1][j],maxValue[i-1][j-w[i]]+P[i]}，其中 w[i] 表示第 i 颗宝石的重量，P[i] 表示第 i 颗宝石的价值。

物理意义：当前背包能装入的最大价值为只有 i-1 个宝石时背包能装入的最大价值 和 腾出第 i 颗宝石重量后剩余背包容量装入 i-1 个宝石的最大价值加上装入第 i 颗宝石价值 的较大值.

public class KnapsackProblem {

    /**
     * @param w 每一个宝石的重量
     * @param v 每一个宝石的价值
     * @param capacity 背包的容量
     */
    public static void solution(int[] w,int[] v,int capacity) {
        //maxValue[i][j]表示前 i 个宝石装到剩余体积为 j 的背包里能达到的最大价值
        int[][] maxValue = new int[w.length][capacity]; 
        //初始化
        for(int j = 0; j < capacity; j++) {
            maxValue[0][j] = 0; //没有宝石时价值为0
        }
        for(int i = 0; i < w.length; i++) {
            maxValue[i][0] = 0; //容量为0时价值为0
        }
        
        for(int i = 1; i < w.length; i++) { //从有1个宝石算起
            for(int j = 1; j < capacity; j++) { //从容量为1算起
                if(w[i] < j) {
                    maxValue[i][j] = Math.max(maxValue[i-1][j],maxValue[i-1][j-w[i]] + v[i]);
                } else {
                    //无法承载此颗宝石重量
                    maxVlue[i][j] = maxValue[i-1][j];
                }
            }
        }
    }
    //打印结果
    for(int i=0;i<6;i++) {
        for(int j=0;j<9;j++) {
            System.out.printf("%-5d",temp[i][j]);
        }
        System.out.println();
    }
}

数据求交集

LeeCode: 给定两个数组，编写一个函数来计算它们的交集。

class Solution {

  public int[] set_intersection(HashSet<Integer> set1, HashSet<Integer> set2) {
    int [] output = new int[set1.size()];
    int idx = 0;
    for (Integer s : set1)
      if (set2.contains(s)) output[idx++] = s;

    return Arrays.copyOf(output, idx);
  }

  public int[] intersection(int[] nums1, int[] nums2) {
    HashSet<Integer> set1 = new HashSet<Integer>();
    for (Integer n : nums1) set1.add(n);
    HashSet<Integer> set2 = new HashSet<Integer>();
    for (Integer n : nums2) set2.add(n);

    if (set1.size() < set2.size()) return set_intersection(set1, set2);
    else return set_intersection(set2, set1);
  }
}

也可以使用retainAll函数：

class Solution {
  public int[] intersection(int[] nums1, int[] nums2) {
    HashSet<Integer> set1 = new HashSet<Integer>();
    for (Integer n : nums1) set1.add(n);
    HashSet<Integer> set2 = new HashSet<Integer>();
    for (Integer n : nums2) set2.add(n);

    set1.retainAll(set2);

    int [] output = new int[set1.size()];
    int idx = 0;
    for (int s : set1) output[idx++] = s;
    return output;
  }
}

复杂度分析

• 时间复杂度：O(m+n)O(m+n)，其中 n 和 m 是数组的长度。O(n)O(n) 的时间用于转换 nums1 在集合中，O(m)O(m) 的时间用于转换 nums2 到集合中，并且平均情况下，集合的操作为 O(1)O(1)。
• 空间复杂度：O(m+n)O(m+n)，最坏的情况是数组中的所有元素都不同。

100G 的文件，只有 100M 内存，对文件进行排序

外部排序 + 多路归并

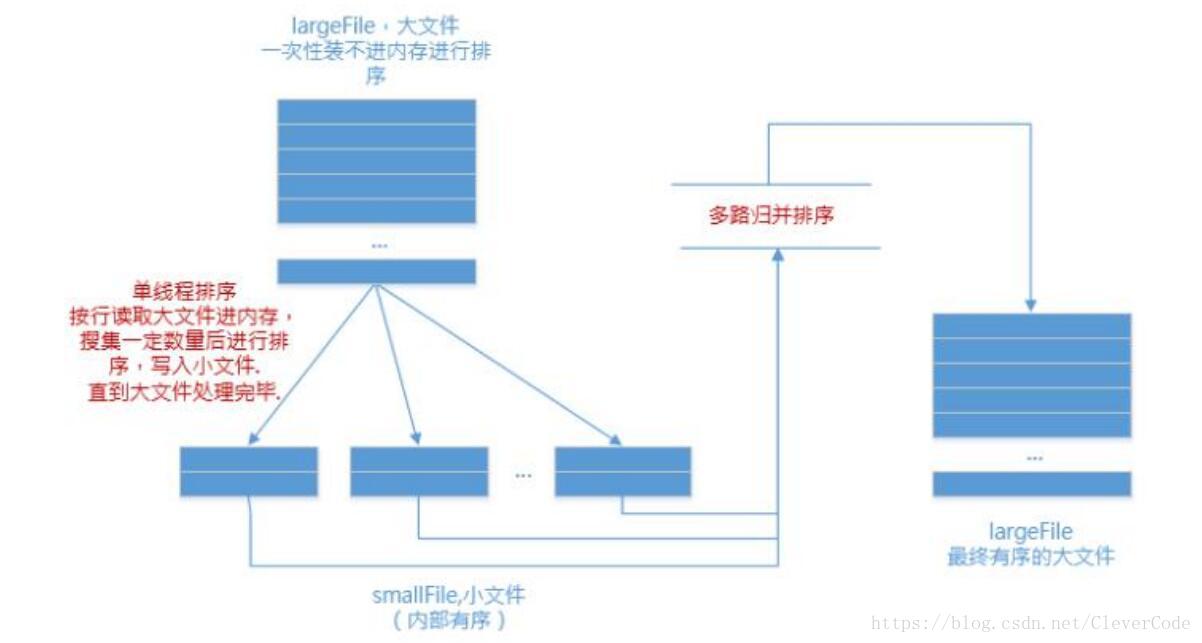
100G 数据，按照 100M 内存拆分，然后排序成有序的数据，然后写入到 file1,file2…file100。

之后进行多路归并排序：

1. 从 file1,file2,file3，…，file100 取出第一个数，即最大或者最小的，所有的初始指针都是第一行。

min1 = min(fil1,file2,file3, … ,file100)；

2. min1 写入到大数据文件,大数据行数指针 + 1,min1 对应的行数指针 +1。
3. 从对应的行指针取出第二个数进行对比，继续归并

位图法

前提是内存容得下这么大的位图。每读一个数，相应的位图位置标 1，如果又重复数，可以建一个数组相应的 count++，遍历完文件之后对对应位置为 1 的输出下标。

100亿个整型数据，乱序，100M内存，求中位数

这里认为是带符号的int,所以4字节，占32位。

假设100亿个数字保存在一个大文件中，依次读一部分文件到内存(不超过内存的限制)，将每个数字用二进制表示，比较二进制的最高位(第32位，符号位，0是正，1是负)，如果数字的最高位为0，则将这个数字写入 file_0 文件中；如果最高位为 1，则将该数字写入 file_1 文件中。

从而将 100 亿个数字分成了两个文件，假设 file_0 文件中有 60亿 个数字，file_1 文件中有 40 亿个数字。那么中位数就在 file_0 文件中，并且是 file_0 文件中所有数字排序之后的第 10 亿个数字。（file_1 中的数都是负数，file_0 中的数都是正数，也即这里一共只有 40 亿个负数，那么排序之后的第 50 亿个数一定位于 file_0 中）

现在，只需要处理 file_0 文件了（不需要再考虑 file_1 文件）。对于 file_0 文件，同样采取上面的措施处理：将 file_0 文件依次读一部分到内存(不超内存限制)，将每个数字用二进制表示，比较二进制的次高位（第31位），如果数字的次高位为 0，写入 file_0_0 文件中；如果次高位为1，写入file_0_1 文件中。

现假设 file_0_0 文件中有30亿个数字，file_0_1 中也有30亿个数字，则中位数就是：file_0_0 文件中的数字从小到大排序之后的第 10 亿个数字。

抛弃 file_0_1 文件，继续对 file_0_0 文件 根据次次高位(第30位) 划分，假设此次划分的两个文件为：file_0_0_0 中有5亿个数字，file_0_0_1 中有25亿个数字，那么中位数就是 file_0_0_1 文件中的所有数字排序之后的第 5 亿个数。

以此类推，直到划分的文件可直接加载进内存时，就可以直接对数字进行快速排序，找出中位数了。

m * n 的格子，部分格子有障碍物，从左上角到右下角有多少条路径

Leecode：一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。现在考虑网格中有障碍物（网格中的障碍物和空位置分别用 1 和 0 来表示，1 代表障碍物）。那么从左上角到右下角将会有多少条不同的路径？

解题思路：动态规划的思想，到达一个格子可以从上方到达，也可以从左边到达，所以分别计算上方和左侧两个格子的到达数相加就是当前格子的路径数。具体如下：

如果格子上有障碍，那么不考虑包含这个格子的任何路径。从左至右、从上至下的遍历整个数组，那么在到达某个顶点之前我们就已经获得了到达前驱节点的方案数，这就变成了一个动态规划问题。我们只需要一个 obstacleGrid 数组作为 DP 数组。

注意： 根据题目描述，包含障碍物的格点有权值 1，我们依此来判断是否包含在路径中，然后我们可以用这个空间来存储到达这个格点的方案数。

算法思路如下：

1. 如果第一个格点 obstacleGrid[0,0] 是 1，说明有障碍物，那么机器人不能做任何移动，我们返回结果 0。
2. 否则，如果 obstacleGrid[0,0] 是 0，我们初始化这个值为 1 然后继续算法。
3. 遍历第一行，如果有一个格点初始值为 1 ，说明当前节点有障碍物，没有路径可以通过，设值为 0 ；否则设这个值是前一个节点的值 obstacleGrid[i,j] = obstacleGrid[i,j-1]。
4. 遍历第一列，如果有一个格点初始值为 1 ，说明当前节点有障碍物，没有路径可以通过，设值为 0 ；否则设这个值是前一个节点的值 obstacleGrid[i,j] = obstacleGrid[i-1,j]。
5. 现在，从 obstacleGrid[1,1] 开始遍历整个数组，如果某个格点初始不包含任何障碍物，就把值赋为上方和左侧两个格点方案数之和 obstacleGrid[i,j] = obstacleGrid[i-1,j] + obstacleGrid[i,j-1]。
6. 如果这个点有障碍物，设值为 0 ，这可以保证不会对后面的路径产生贡献。

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {

        int R = obstacleGrid.length;
        int C = obstacleGrid[0].length;

        if (obstacleGrid[0][0] == 1) {
            return 0;
        }

        obstacleGrid[0][0] = 1;

        //遍历第一列
        for (int i = 1; i < R; i++) {
            obstacleGrid[i][0] = (obstacleGrid[i][0] == 0 && obstacleGrid[i - 1][0] == 1) ? 1 : 0;
        }

        //遍历第一行
        for (int i = 1; i < C; i++) {
            obstacleGrid[0][i] = (obstacleGrid[0][i] == 0 && obstacleGrid[0][i - 1] == 1) ? 1 : 0;
        }

        for (int i = 1; i < R; i++) {
            for (int j = 1; j < C; j++) {
                if (obstacleGrid[i][j] == 0) {
                    obstacleGrid[i][j] = obstacleGrid[i - 1][j] + obstacleGrid[i][j - 1];
                } else {
                    obstacleGrid[i][j] = 0;
                }
            }
        }

        //返回最后一格的值
        return obstacleGrid[R - 1][C - 1];
    }
}

• 时间复杂度 ： O(M×N) 。长方形网格的大小是 M×N，而访问每个格点恰好一次。
• 空间复杂度 ： O(1)。我们利用 obstacleGrid 作为 DP 数组，因此不需要额外的空间

分5个线程计算1-10000的和，要求全部计算完了再汇总

import java.util.concurrent.CountDownLatch;
import java.util.concurrent.ExecutorService;
import java.util.concurrent.Executors;

public class Solution {
    public static void main(String[] args) {
        CountDownLatchApply countDownLatchApply = new CountDownLatchApply();
        long l1 = System.currentTimeMillis();
        countDownLatchApply.getTotal2();
        long l2 = System.currentTimeMillis();
        System.out.println("循环遍历:" + (l2-l1));

        long l3 = System.currentTimeMillis();
        countDownLatchApply.getTotal();
        long l4 = System.currentTimeMillis();
        System.out.println("countDownLatch:" + (l4-l3));
    }

    public void getTotal2() {
        int result = 0;
        for (int i = 1; i <= 1000000; i++) {
                result += i;
        }
        System.out.println("循环遍历结果：" + result);
    }

    public void getTotal() {
        final int totalCount = 5;
        CountDownLatch countDownLatch = new CountDownLatch(totalCount);
        ExecutorService executorService = Executors.newCachedThreadPool();
        int[] total = new int[5];
        int result = 0;
        for (int i = 0; i < totalCount; i++) {
            int finalI = i;
            executorService.execute(()->{
                int sum = 0;
                for (int j = 1; j <= 200000; j++) {
                    sum += (j + finalI*200000);
                }
                total[finalI] = sum;
                countDownLatch.countDown();
            });
        }
        try {
            countDownLatch.await(); //main线程会阻塞在这里
        } catch (InterruptedException e) {
            e.printStackTrace();
        }
        for (int i = 0; i < 5; i++) {
            result += total[i];
        }
        System.out.println("countDownLatch结果：" + result);
    }
}

合并区间

Leecode：给出一个区间的集合，请合并所有重叠的区间

示例 1:
输入: [[1,3],[2,6],[8,10],[15,18]]
输出: [[1,6],[8,10],[15,18]]
解释: 区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

示例 2:
输入: [[1,4],[4,5]]
输出: [[1,5]]
解释: 区间 [1,4] 和 [4,5] 可被视为重叠区间。

解题思路：

首先，我们将列表根据区间开始范围从小到大进行排序。然后，将第一个区间插入 merged 数组中，然后按顺序考虑之后的每个区间：如果当前区间的左端点在前一个区间的右端点之后，那么他们不会重合，可以直接将这个区间插入 merged 中；否则，他们重合，将当前区间的右端点更新为前一个区间的右端点 end 值和当前右端点值较大的一个，完成合并。

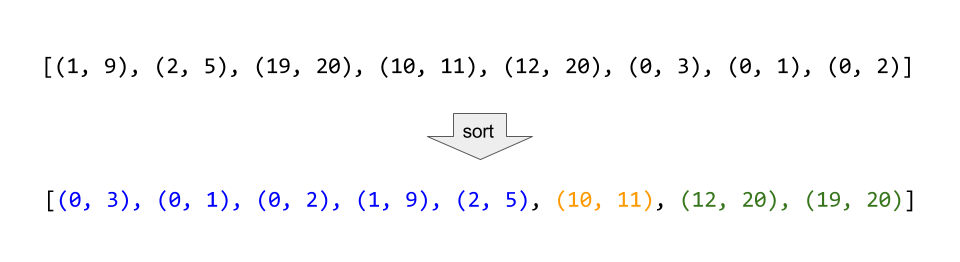
代码实现

import java.util.Arrays;
import java.util.Comparator;
import java.util.LinkedList;

public class MergeInterval {

    public int[][] merge(int[][] intervals) {

        Arrays.sort(intervals, new Comparator<int[]>() {
            @Override
            //从小到大排序
            public int compare(int[] o1, int[] o2) {
                return o1[0] - o2[0];
            }
        });

        LinkedList<int[]> list = new LinkedList<>();
        for(int[] interval : intervals) {
            if(list.isEmpty() || list.getLast()[1] < interval[0]) {
                list.add(interval);
            } else {
                list.getLast()[1]  = Math.max(list.getLast()[1],interval[1]);
            }
        }
        return list.toArray(new int[0][2]);
    }
}

复杂度分析

• 时间复杂度：O(nlogn)，除去 sort 的开销，只需要一次线性扫描，所以主要的时间开销是排序的 O(nlgn)

• 空间复杂度：O(1) (or O(n))，如果可以原地排序 intervals ，就不需要额外的存储空间；否则，就需要一个线性大小的空间去存储 intervals 的备份，来完成排序过程。

股票的最大利润

Leecode：给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。

如果你最多只允许完成一笔交易（即买入和卖出一支股票一次），设计一个算法来计算你所能获取的最大利润。

示例 1:

输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
     注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

示例 2:

输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

解题思路：

假设第 i 轮进行卖出操作，买入操作价格应该在 i 之前并且价格最低。

class Solution {
    public int maxProfit(int[] prices) {
        if(prices == null || prices.length == 0) {
            return 0;
        }
        int minPrice = prices[0];
        int maxProfit = 0;
        for(int i = 1; i < prices.length; i++) {
            minPrice = Math.min(minPrice,prices[i]);
            maxProfit = Math.max(maxProfit,prices[i] - minPrice);
        }
        return maxProfit;
    }
}

复杂度分析

• 时间复杂度：O(n)，只需要遍历一次。
• 空间复杂度：O(1)，只使用了常数个变量。

滑动窗口的最大值

Leecode：给定一个数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回滑动窗口中的最大值。

示例：

输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7] 
解释: 

  滑动窗口的位置                最大值
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

解题思路：

动态规划：算法的思想是将输入数组分割成有 k 个元素的块。若 n % k != 0，则最后一块的元素个数可能更少。

开头元素为 i ，结尾元素为 j 的当前滑动窗口可能在一个块内，也可能在两个块中。

建立数组 left， 其中 left[j] 是从块的开始到下标 j 最大的元素，方向左->右。
建立数组 right，其中 right[j] 是从块的结尾到下标 j 最大的元素，方向右->左。

两数组一起可以提供两个块内元素的全部信息。考虑从下标 i 到下标 j 的滑动窗口。 根据定义，right[i] 是左侧块内的最大元素， left[j] 是右侧块内的最大元素。因此滑动窗口中的最大元素为 max(right[i], left[j])。

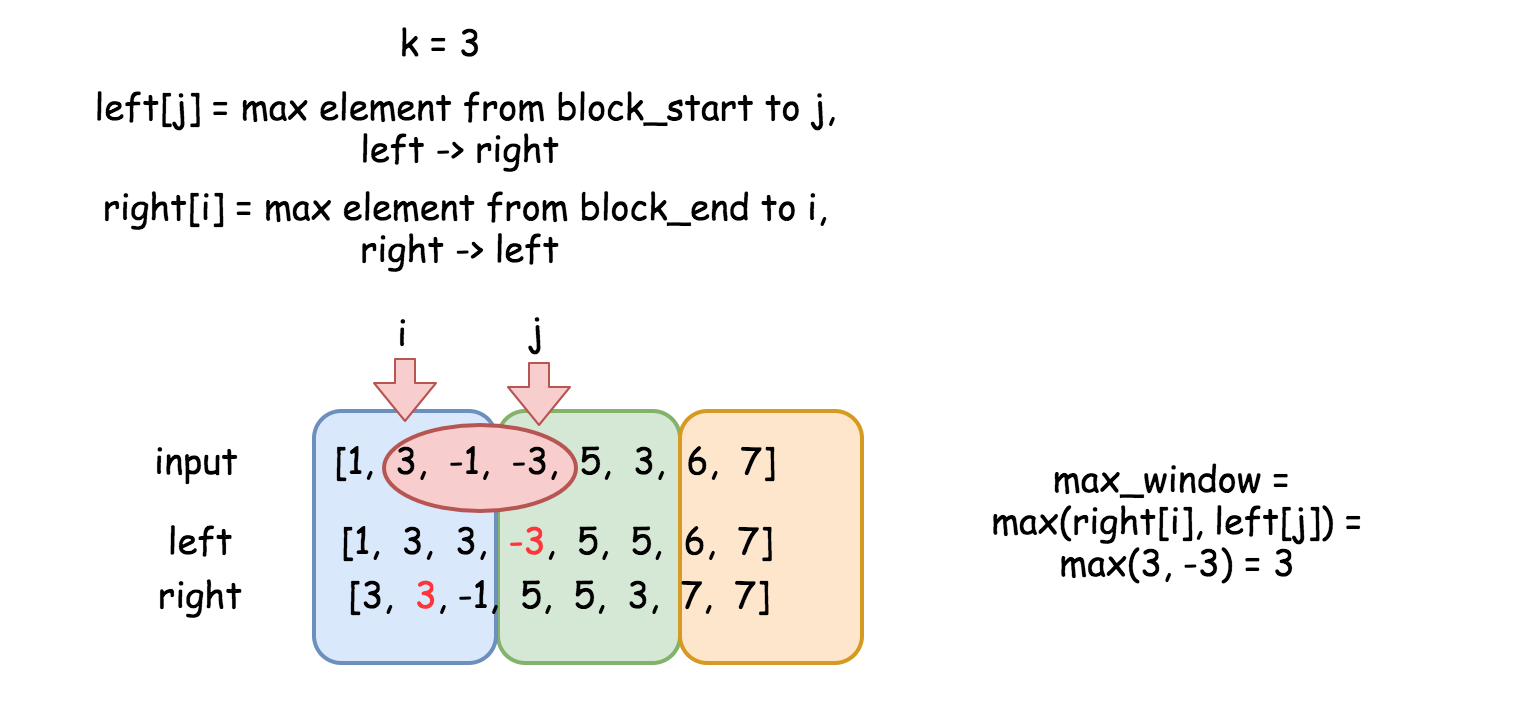
算法流程如下：

1. 从左到右遍历数组，建立数组 left。
2. 从右到左遍历数组，建立数组 right。
3. 建立输出数组 max(right[i], left[i + k - 1])，其中 i 取值范围为 (0, n - k + 1)。

class Solution {
  public int[] maxSlidingWindow(int[] nums, int k) {
    int n = nums.length;
    if (n * k == 0) return new int[0];
    if (k == 1) return nums;

    int [] left = new int[n];
    left[0] = nums[0];
    int [] right = new int[n];
    right[n - 1] = nums[n - 1];
    for (int i = 1; i < n; i++) {
      // from left to right
      if (i % k == 0) left[i] = nums[i];  // block_start
      else left[i] = Math.max(left[i - 1], nums[i]);

      // from right to left
      int j = n - i - 1;
      if ((j + 1) % k == 0) right[j] = nums[j];  // block_end
      else right[j] = Math.max(right[j + 1], nums[j]);
    }

    int [] output = new int[n - k + 1];
    for (int i = 0; i < n - k + 1; i++)
      output[i] = Math.max(left[i + k - 1], right[i]);

    return output;
  }
}

盛最多水的容器

Leetcode 11 题

给 n 个非负整数 a1，a2，…，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

说明：不能倾斜容器。

示例1:

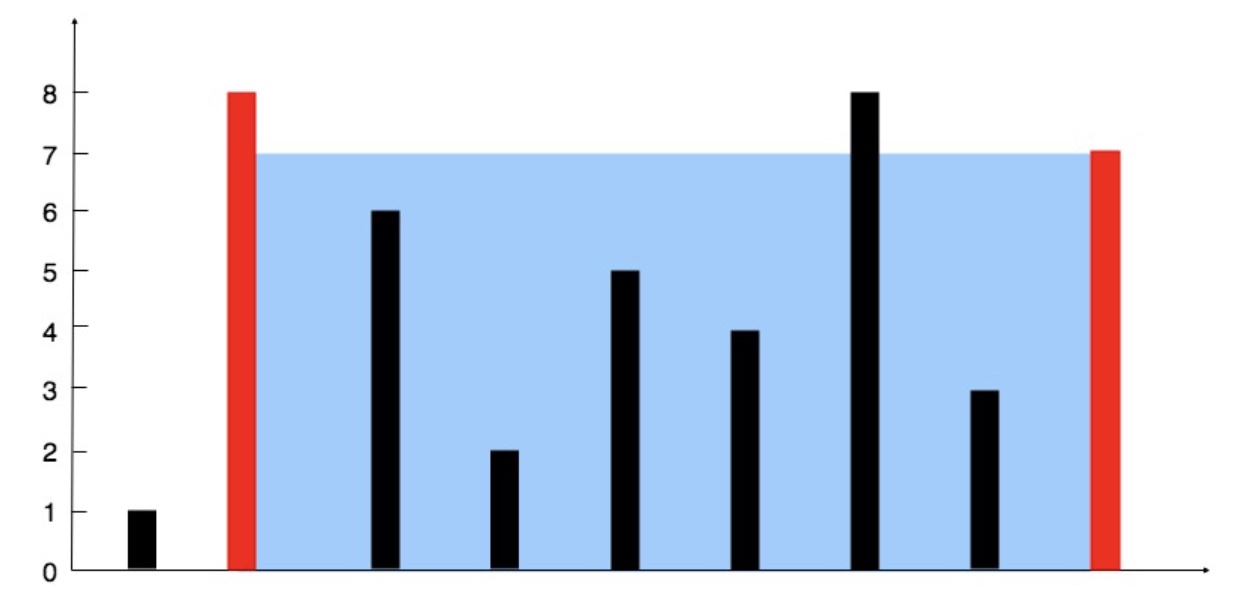
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例2:

输入：height = [1,1]
输出：1

示例3:

输入：height = [4,3,2,1,4]
输出：16

示例4:

输入：height = [1,2,1]
输出：2

解题思路

此题需要使用双指针的解法（第一次看到这道题完全没思路…）。

题目中的示例为：

[1, 8, 6, 2, 5, 4, 8, 3, 7]
 ^                       ^

在初始时，左右指针分别指向数组的左右两端，它们可以容纳的水量为 min(1,7)∗8=8。

此时我们需要移动一个指针。移动哪一个呢？应该移动对应数字较小的那个指针（即此时的左指针）。这是因为，由于容纳的水量是由 两个指针指向的数字中较小值 * 指针之间的距离决定的。如果我们移动数字较大的那个指针，那么前者两个指针指向的数字中较小值不会增加，后者指针之间的距离会减小，那么这个乘积会减小。因此，我们移动数字较大的那个指针是不合理的。因此，我们移动数字较小的那个指针。

所以，我们将左指针向右移动：

[1, 8, 6, 2, 5, 4, 8, 3, 7]
    ^                    ^

此时可以容纳的水量为 min(8,7)∗7=49。由于右指针对应的数字较小，我们移动右指针：

[1, 8, 6, 2, 5, 4, 8, 3, 7]
    ^                 ^

此时可以容纳的水量为min(8,3)∗6=18。由于右指针对应的数字较小，我们移动右指针：

[1, 8, 6, 2, 5, 4, 8, 3, 7]
    ^              ^

此时可以容纳的水量为 min(8,8)∗5=40。两指针对应的数字相同，我们可以任意移动一个，例如左指针：

[1, 8, 6, 2, 5, 4, 8, 3, 7]
       ^           ^

此时可以容纳的水量为 min(6,8)∗4=24。由于左指针对应的数字较小，我们移动左指针，并且可以发现，在这之后左指针对应的数字总是较小，因此我们会一直移动左指针，直到两个指针重合。在这期间，对应的可以容纳的水量为：min(2,8)∗3=6，min(5,8)∗2=10，min(4,8)∗1=4。

在我们移动指针的过程中，计算到的最多可以容纳的数量为 4949，即为最终的答案。

代码实现

func maxArea(height []int) int {
    // 声明左右指针
    lp := 0
    rp := len(height) - 1
    // 初始化最大容量
    maxContain := 0

    // for循环直到左右指针重合
    for lp != rp {
        // 计算容量
        curContain := math.Min(float64(height[lp]), float64(height[rp])) * float64(rp-lp)
        maxContain = int(math.Max(float64(maxContain), curContain))

        // 移动对应数值较小的指针
        if height[lp] < height[rp] {
            lp++
        } else {
            rp--
        }
    }
    return maxContain
}

电话号码的字母组合

Leetcode 17 题

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按任意顺序返回。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例 1：

输入：digits = "23"
输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]

示例 2：

输入：digits = ""
输出：[]

示例 3：

输入：digits = "2"
输出：["a","b","c"]

解题思路

这道题在一看到要求拿到全部组合的时候，就应该联想到广度优先和深度优先这两种遍历的思路。

深度优先的解法就是通过递归来进行，而广度优先则是借助于队列来实现。

代码实现

var phoneMap map[string]string = map[string]string{
    "2": "abc",
    "3": "def",
    "4": "ghi",
    "5": "jkl",
    "6": "mno",
    "7": "pqrs",
    "8": "tuv",
    "9": "wxyz",
}

var results []string
// 深度优先
func letterCombinations1(digits string) []string {
    if len(digits) == 0 {
        return []string{}
    }
    results = []string{}
    recursion(digits,0,"")
    return results
}

func recursion(digits string, index int, currentResult string) {
    if index == len(digits) {
        results = append(results, currentResult)
        return
    }
    currentNum := string(digits[index])
    chars := phoneMap[currentNum]
    for i := 0; i < len(chars); i++ {
        recursion(digits, index+1, currentResult+string(chars[i]))
    }
    return
}

// 广度优先
func letterCombinations2(digits string) []string {
    if len(digits) == 0 {
        return []string{}
    
    resultQueue  := []string{""}
    for i := 0; i < len(digits); i++ {
        currentNum := string(digits[i])
        chars := phoneMap[currentNum]
        currentQueueLen := len(resultQueue)
        for j := 0; j < currentQueueLen; j++ {
            tmpResult := resultQueue[0]
            resultQueue = resultQueue[1:]
            for k := 0; k < len(chars); k++ {
                resultQueue = append(resultQueue,tmpResult + string(chars[k]))
            }
        }
    }
    return resultQueue
}

参考内容

主要参考以来两篇博客以及相关博客推荐，因找的博客比较多，没注意记录，最后好多忘了在哪2333，如果有侵权，请及时联系我，非常抱歉。
https://github.com/Snailclimb/JavaGuide
https://github.com/CyC2018/CS-Notes
100G 数据，只有 100M 内存，怎么排序
求比n小的一个数，使其各位数的乘积最大
牛客网——腾讯WXG后端一面面经
完全二叉树的叶子节点总数问题
【面试被虐】说说游戏中的敏感词过滤是如何实现的？